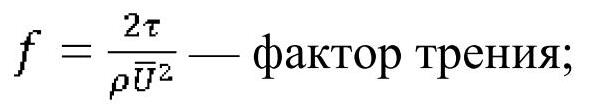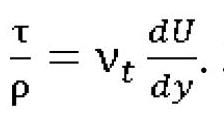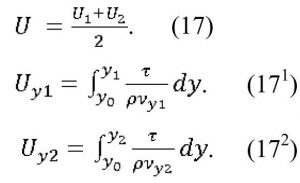Сегодня, 8 февраля
- (Нет мероприятий)
Ближайшие мероприятия
-
10 февраля - 13 февраляНовосибирскСибирская строительная неделя
-
16 февраля - 19 февраля
-
10 марта - 12 марта
-
20 марта - 22 мартаСанкт-ПетербургВыставка «Строим загородный дом»
-
24 марта - 26 марта
-
31 марта - 03 апреляМоскваВыставка MosBuild 2026
Модель и полуэмпирический метод расчета пристенной турбулентности
А. П. Рафалович, научный консультант АО «НПО «Тепломаш»
Проектирование инженерных систем для создания определенных климатических условий всегда связано с оптимизацией теплообменной аппаратуры, требующей расчетов гидродинамики, а также массо- и теплообмена. Практически все такие аппараты работают в турбулентных режимах.
Несмотря на наличие в уравнениях турбулентного движения (уравнениях Рейнольдса) дополнительных неизвестных, делающих систему уравнений незамкнутой, расчет турбулентных потоков не представляется неразрешимой задачей благодаря быстродействующим компьютерам и значительному количеству опытных данных. Однако для получения оптимизационных решений, связанных с изменением не только геометрии, но и самой теплообменной поверхности (как, например, при выборе оптимальной шероховатости), каждый новый аппарат, так же как и новая поверхность, должны быть экспериментально проверены, что не только усложняет оптимизацию, но порой делает ее невозможной. Это касается расчета как сопротивления, так и массо- и теплообмена. Поэтому создание обобщенной модели турбулентного течения, применимой для различных поверхностей и контуров обтекаемых тел, остается крайне важной задачей.
Широко известна двуслойная модель Прандтля [1], в которой турбулентный поток разбивается на вязкий подслой и турбулентное ядро. Эта модель дает удовлетворительные результаты для расчета сопротивления и поля скоростей в турбулентном ядре на пластинах и в трубах. Для расчетов массо- и теплообмена Карман предложил трехслойную модель [2], содержащую также переходную область от вязкого подслоя к турбулентному ядру, которая, наряду с вязким подслоем, является крайне важной как при гидродинамических расчетах, так и при расчетах массо- и теплообмена. Модель Кармана позволила расширить область применения аналогии Рейнольдса между переносом импульса и переносом тепла и массы, но заложенные в нее константы не универсальны. Поэтому при решении прикладных задач наибольшее распространение получили модели, основанные на различных допущениях о степенной зависимости турбулентной вязкости от расстояния до стенки. Как пример можно привести модели Ландау [3] и Левича [4].
В основе излагаемой ниже модели лежит следующая гипотеза. Турбулентные пульсации из внешней части пограничного слоя проникают в вязкий подслой. Вязкий подслой получает дополнительное количество движения от привнесенной этими пульсациями жидкости. Часть вязкого подслоя, в виде вихря, отрывается и расширяется в направлении внешней части погранслоя. Таким образом, в турбулентном погранслое наблюдается два типа возмущений: пульсации из ядра погранслоя, являющиеся причиной срывов части вязкого подслоя, которые, в свою очередь, генерируют другой тип возмущений — пульсации из вязкого подслоя. Последние привносят в ядро погранслоя энергию, связанную с трением на обтекаемой поверхности, и, таким образом, поддерживают турбулентное пульсационное движение во внешней части погранслоя.
Впервые предположение о воздействии на параметры турбулентного погранслоя пульсаций с двумя различными характерными масштабами было сделано Маньковским, Марром и Рафаловичем в главе 4 монографии [5]. К сожалению, в работе [5] авторы, в число которых входит и автор настоящей работы, не сумели довести предложенную модель до расчета поля осредненных скоростей в трубе и на пластине, что повлияло на точность и область применения предложенных расчетных зависимостей.
В настоящей работе приводятся результаты расчета и моделирования турбулентного потока, выполненные на основе предлагаемой модели для труб с гладкой и шероховатой поверхностью, а также для течения при обтекании гладких и шероховатых пластин.
Присвоим пульсациям из ядра потока индекс 1. Эти пульсации имеют внутренний масштаб δ1. Пульсации из вязкого подслоя, с индексом 2, имеют внутренний масштаб δ2. Внутренним масштабом здесь называется размер такого вихря, в котором кажущаяся турбулентная вязкость равна кинематической вязкости жидкости. Оба типа пульсаций действуют периодично. Часть периода доминируют пульсации с внутренним масштабом δ1, которые обретают форму вихрей малого диаметра, приносящих с собой в вязкий подслой вместе с массой жидкости и ее скорость, сопоставимую со скоростью переходного подслоя. Соприкасаясь около стенки с вязким подслоем, вихри с внутренним масштабом δ1 замедляются до скорости вязкого подслоя. Замедление вихрей с внутренним масштабом δ1 приводит к повышению давления и, в конечном итоге, к отрыву участка вязкого подслоя с внутренним масштабом δ2. Вязкий подслой определяется безразмерной толщиной y0/d и безразмерным параметром η0:
η0 = y0 U*/ν, (1)
где y0 — расстояние от поверхности до верхней границы вязкого подслоя;
d — внутренний диаметр трубы;
ν — молекулярная (кинематическая) вязкость;
U* = (τст/ρ)1/2 = (f/2)1/2 Ū — динамическая скорость;
τст — касательное напряжение на стенке;
ρ — плотность жидкости;
Ū — скорость жидкости на внешней границе погранслоя для пластины или среднерасходная скорость жидкости для трубы. В другой форме равенство (1) можно записать, как
η0 = (y0/d) (f/2)1/2Re. (11)
Эксперименты с визуализацией погранслоя [6], [7] показали, что при отрыве вязкий подслой теряет примерно половину толщины. Учитывая это, модель, предложенная в настоящей работе, предполагает, что вязкий подслой состоит из двух частей: первая, квазиламинарная часть, прилегающая к стенке, с постоянной при заданном числе Re толщиной y0/2, и вторая часть с переменной по времени толщиной, меняющейся от 0 до δ20. При этом среднестатистическая высота всего вязкого подслоя равняется величине y0, т. е. удвоенной толщине пристеночной квазиламинарной части. Мгновенная толщина потока жидкости в вязком подслое периодически меняется. После отрыва из переходного подслоя в вязкий подслой проникают вихри с внутренним масштабом δ1. Эти вихри привносят поток импульса к оставшейся, квазиламинарной части подслоя. Вязкий подслой утолщается, пока привнесенная часть не достигнет критической толщины δ20, после чего срывается в виде исходящих из вязкого подслоя вихрей. Оторвавшиеся вихри при движении к внешней части погранслоя расширяются и переходят в пульсации с внутренним масштабом δ2.
Одной из важнейших характеристик турбулентного погранслоя является введенное Буссинеском понятие кажущейся турбулентной вязкости νt. Введение νt позволило описать касательное напряжение при турбулентном движении аналогично касательному напряжению в ламинарном потоке, как
Легко показать, что из предложенной Прандтлем логарифмической зависимости безразмерной осредненной по времени скорости в ядре турбулентного погранслоя от безразмерного расстояния до стенки, φ = ln η + C, следует линейная зависимость турбулентной вязкости от расстояния от стенки:
Можно также предположить, что в модели, где рассматриваются два типа пульсаций, кажущаяся турбулентная вязкость обоих типов также линейно зависит от расстояния до стенки как в вязком, так и в переходном подслое. Учитывая, что кажущаяся турбулентная вязкость пульсаций внутреннего масштаба d равна кинематической вязкости жидкости
получим
Следуя предположению о периодичном характере пульсаций в верхней части вязкого подслоя и в переходном подслое, выражение для определения касательного напряжения можно представить, как
Коэффициенты a и b в выражении (3) отражают периодичность и взаимовлияние пульсаций. Если пульсации действуют по очереди с одинаковым по времени периодом, то a = b = 0.5, и средняя по времени скорость в сечении у определяется как U=0,5 (U1+U2) . Если пульсации действуют совместно, U1=U2 и турбулентные вязкости в выражении (3) можно просуммировать. Если пульсации часть времени действуют вместе, а часть — попеременно, коэффициенты a и b отражают время попеременного действия пульсаций, а при равенстве скоростей U1 и U2 — время их совместного действия.
Из уравнения (3) можно также вывести следующую зависимость для коэффициента переноса импульса или фактора трения f:
Положим, что внутренний масштаб пульсаций в ядре потока δ1 отвечает соотношению δ1 ~ ν3/4 ԑ-1/4, где ԑ — поток диссипации, т. е. закону ¾. Тогда безразмерный внутренний масштаб δ1/d пропорционален Re-3/4. Относительно вихрей, отрывающихся из вязкого подслоя, можно предположить, что безразмерный масштаб δ2/d пропорционален толщине вязкого подслоя [см. уравнение (1)], т. е. δ2/d ~ f -1/2Re-1, и уравнение (4) можно переписать следующим образом:
f Re = A1 f n Re 3/4 + B1 f1/2 Re. (5)
Из опытных данных и расчетных зависимостей для гладкой трубы были найдены постоянные n = 1/4, A1 = 1/6 и B1 = 1/32. Разделим также обе части уравнения (5) на 2Re
(f /2) = 0.099 (f/2)1/4 Re-1/4 + 0.0221 (f/2)1/2. (51)
Если сократить теперь обе части уравнения (51) на (f/2)1/2, получим более удобное уравнение для коэффициента сопротивления в гладкой трубе:
Табл. 1 демонстрирует точность формул (1) и (2) в сравнении с эмпирической формулой Прандтля (по опытным данным Никурадзе): f = [4 lg (2 Re*f1/2) – 1.6]-2.
| Таблица 1. Значения фактора трения f при различных числах Re | |||
| Число Re | Формула (6) | Закон сопротивления Прандтля | Расхождение, % |
| 4.00E+03 | 0.00963 | 0.00998 | -3.50% |
| 1.00E+04 | 0.00768 | 0.00772 | -0.55% |
| 3.00E+04 | 0.00593 | 0.00587 | 0.99% |
| 1.00E+05 | 0.00454 | 0.00450 | 0.93% |
| 3.00E+05 | 0.00364 | 0.00362 | 0.66% |
| 1.00E+06 | 0.002914 | 0.00291 | 0.08% |
| 3.00E+06 | 0.002433 | 0.00243 | 0.10% |
| 1.00E+07 | 0.002044 | 0.00203 | 0.89% |
Данные табл. 1 показывают, что результаты расчета по уравнению (6) хорошо согласуются с результатами расчетов по эмпирическому уравнению Прандтля в диапазоне Re = 104 – 107.
Помимо прочего, необходимо подчеркнуть, что формула Прандтля f = [4 lg (2 Ref1/2) – 1.6]-2 при очень больших числах Re теряет физический смысл, поскольку предел, к которому стремится фактор трения при Re → ∞, f → 1/Re, означает, что при очень больших числах Re поток импульса растет медленнее, чем квадрат скорости. В отличие от формулы Прандтля, согласно зависимости (6), при устремлении числа Re к бесконечности f → f min = 9.77*10-4, а уравнение (6) принимает вид:
(f min/2)1/2 = 0.0221. (61)
Логарифмический характер зависимости безразмерной скорости от безразмерного расстояния до стенки в ядре погранслоя хорошо известен. Для вычисления поля скоростей в промежуточном подслое рассмотрим сначала вязкий подслой. Согласно классической модели Прандтля, Шлихтинга и пр., безразмерный параметр вязкого подслоя η0 является константой, а средняя безразмерная высота вязкого подслоя (y0/d) зависит от (f/2)-1/2 и числа Re-1. Как упоминалось выше, постоянная часть подслоя, имеющая среднюю толщину у0/2, во многом формируется пульсациями с внутренним масштабом δ1, и, при заданном числе Re, эта толщина определяется как
(y0/d)/2 = (А0/2) (f/2)-1/2 Re-1. (7)
В свою очередь, переменная часть вязкого подслоя формирует пульсации масштаба вязкого подслоя δ20, который следует зависимости:
(δ20/d) = В0Re-1. (8)
В равенствах (7), (8) А0 и В0 — константы.
Для нахождения связи между у0 и δ20 и, соответственно, между константами А0 и В0 обратимся к уравнению (6). Если умножить обе части уравнения (6) на комплекс В0(f/2)-1/2Re-1, получим равенство:
В0Re-1 = 0.099 В0 (f/2)-3/4 Re-5/4 + 0.0221 В0 (f/2)-1/2 Re-1. (9)
При Re → ∞ первым слагаемым в правой части можно пренебречь, откуда:
В0Re-1 = 0.0221 В0 (f/2)-1/2 Re-1. (10)
Заменяя левую часть равенства (10) на (δ20/d) из (8), т. е. на половинную толщину вязкого подслоя, получим следующую связь между константами А0 и В0: А0 = 0.0442 В0 . Из равенств (11) и (7) следует ηу0 = А0. Общепринятая величина безразмерного параметра ηу0 = 5. Отсюда А0 = 5, В0 = 113.
Принимая, что кажущаяся турбулентная вязкость по мере удаления от стенки линейно возрастает, для турбулентной вязкости пульсаций, генерируемых в вязком подслое ν20, можно записать
ν20 = ν (y/δ20) = В0-1 ν (y/d) Re =0.00884 ν (y/d) Re. (11)
Как показывает опыт, средняя скорость жидкости в вязком подслое линейно зависит от расстояния до стенки. Формула φ = η, где безразмерный параметр скорости φ = U/U*, хорошо работает во всей области вязкого подслоя, включая верхний участок, где турбулентная вязкость внутреннего масштаба каждой из пульсаций имеет вязкость, равную молекулярной кинематической вязкости жидкости и в течение периода формирования, и отрыва переменной области вязкости подслоя, турбулентная вязкость вихрей обоих масштабов попеременно заменяет собой кинетическую вязкость жидкости.
В принципе, формулы (5), (6), где слагаемые определяются масштабами соответствующих пульсаций [см. уравнение (4)], отражают периодичность чередования этих пульсаций. В качестве еще одного, хотя и косвенного, доказательства предлагаемой модели приложим формулу (5) к вычислению теплоотдачи. Поскольку при малых числах Прандтля (Pr) толщина теплового пограничного слоя значительно больше, чем диффузионного, теплоотдача в такой жидкости будет следовать логарифмическому закону ядра потока. Для жидкостей со средним (Pr ≈ 1) и, особенно, с большим (Pr >> 1) числом Прандтля, когда весь тепловой пограничный слой находится в вязкой части гидродинамического подслоя, теплоотдача должна следовать уравнению (51). Подсчитаем число Nu по уравнению, вытекающему из уравнения (51), сохраняя все постоянные:
Nu = 0.099 f ¼ Pr ¼ Re3/4 + 0.0221 f1/2 Pr1/2Re. (12)
Табл. 2 демонстрирует результаты расчета по формуле (12) в сравнении с эмпирическими данными Кутателадзе [8].
Таблица 2. Число Nu при различных значениях чисел Pr и Re
| Источник | Pr | |||||||||
| 0.7 | 1 | 10 | 100 | 200 | ||||||
| Re | ||||||||||
| 104 | 106 | 104 | 106 | 104 | 106 | 104 | 106 | 104 | 106 | |
| Кутателадзе [8] | 37.7 | 1200 | 39.5 | 1440 | 96.5 | 5020 | 198.0 | 11 500 | 238 | 14 100 |
| Кутателадзе [8] | 31.1 | 1150 | 36.5 | 1450 | 89 | 4890 | 196.0 | 12 000 | 248 | 15 300 |
| Кутателадзе [8] | 31.6 | 1260 | 36.5 | 1450 | 89.5 | 3640 | 230.0 | 9150 | 304 | 12 000 |
| Среднее по данным Кутателадзе [8] | 33.5 | 1203 | 37.5 | 1447 | 91.7 | 4517 | 208 | 10 883 | 263 | 13 800 |
| По уравнению (12) | 34 | 1265 | 38.3 | 1455 | 87.1 | 3755 | 215.0 | 10370 | 286 | 14230 |
Данные табл. 2 демонстрируют, что вычисления по уравнению (12) дают очень близкие значения к осредненным значениям эмпирических уравнений, приведенных в монографии [8]. Кроме того, ни один результат из уравнения (12) не выходит из зоны разброса данных [8].
Переходный подслой расположен между верхней границей вязкого подслоя у0 и нижней границей турбулентного ядра у1. В этом подслое также действуют пульсации обоих масштабов: с внутренним масштабом δ2, исходящие из вязкого подслоя, и с внутренним масштабом δ1, формирующиеся в турбулентном ядре. В вязком подслое, где пульсации периодически сменяют одна другую, нужно рассматривать турбулентную вязкость в каждом из полупериодов. Однако, поскольку, начиная с верхней границы вязкого подслоя, размер вихрей увеличивается, пульсации начинают действовать не только поочередно, но и одновременно, сначала частично, а к верхней границе переходного подслоя пульсаций сливаются в единое целое. Соответственно вязкость, начиная с верхней границы переходного подслоя, выражается следующим образом:
νу1 = ν11 + ν21. (13)
Согласно уравнению (2) турбулентные вязкости на верхней границе переходного подслоя у1:
ν11 = (у1/d) ν (С1)-1 (f/2) -1/4 Re3/4. (14)
ν21 = ν (у1/δ2) = 0.00884 (у1/ d) ν Re. (141)
Подставим вязкости, обусловленные обеими пульсациями, в уравнение (13). Поскольку молекулярная вязкость на границе переходного подслоя и ядра погранслоя много меньше каждой из составляющих турбулентной вязкости, этой вязкостью можно пренебречь.
νу1 = (у1/d) ν (С1)-1 (f/2) -1/4 Re3/4 + 0.00884(у1/ d) ν Re1. (15)
Для нахождения двух неизвестных у1 и С1 обратимся к уравнению (6), перемножив все слагаемые на К (у1/d) ν (f/2) 1/4 Re:
К (у1/d) (f/2)1/2 ν Re = 0.099 К (у1/d) ν (f/2) -1/4 Re3/4 + 0.0221К (у1/d) ν Re). (16)
Сравнивая вторые слагаемые в правой части уравнений (15) и (16), получим К = 0.4, а из сравнения первых слагаемых правой части С1 = 25.25.
Для нахождения координаты верхней границы переходного подслоя у1 обратимся опять к модели взаимодействия обоих типов пульсаций. Согласно модели пульсации с внутренним масштабом δ1 срывают часть вязкого подслоя, генерируя вихри, переходящие в пульсации с внутренним масштабом δ2, которые, в свою очередь, поддерживают пульсации с внутренним масштабом δ1. Можно предположить, что переход потока из ламинарного движения в турбулентное связан с возможностью реализации этой цепочки. Отсюда следует, что начало турбулентного движения совпадает с моментом, когда координата у1 оказывается внутри погранслоя. Для гладкой круглой трубы это значит, что при достижении критического числа Рейнольдса (Reкр) соблюдается равенство у1 = d/2. Безразмерный параметр η(d/2) = (f/2)1/2Re/2. Общепринято, что в трубах переход от ламинарного течения к турбулентному происходит при Reкр в диапазоне между 1800 и 2300. Экспериментальные данные, приведенные в монографии Шлихтинга [1], показывают, что и в гладких, и в шероховатых трубах Reкр ≈ 2000, причем в точке перехода коэффициент трения при чисто ламинарном движении равен коэффициенту трения в турбулентном движении. Далее, начиная от Reкр, фактор трения f увеличивается, достигая при Re ≥ 3500 значений, соответствующих уравнению (6), a также решениям Прандтля, Кармана, Блазиуса и др. Логично предположить, что при Re = Reкр в потоке сначала действуют только пульсации из внешней части погранслоя, к которым при дальнейшем росте числа Рейнольдса Re в диапазоне от Reкр до Re = 3500 добавляются и пульсации из вязкого подслоя. Для нахождения переходного числа Reкр оставим в уравнении (51) только первое слагаемое:
(f /2) = 0.099 (f/2)1/4 Reкр-1/4. (52)
Расчет показывает, что равенство между фактором трения по (52) и фактором трения при ламинарном движении в трубе f =16/Re соблюдается при Reкр = 1950. Подставляя это значение в параметр ηу1, получим η(d/2) = 63.
Поле скоростей в переходном подслое
Как упоминалось выше, в вязком подслое и на нижней границе переходного подслоя оба типа пульсаций действуют попеременно, сменяя друг друга. На верхней границе переходного подслоя и в ядре погранслоя оба типа пульсаций действуют одновременно. Если в течение периода время действия каждой из пульсаций одинаково, то при попеременной смене пульсаций скорость потока определяется по среднему значению
Здесь νy1 и νy2 — турбулентные вязкости вихрей с внутренними масштабами δ1 и δ2.
Когда пульсации действуют совместно, скорость определяется из выражения
Для построения профиля осредненной скорости нужно знать, какую часть времени занимают пульсации, действующие независимо, и какую часть — пульсации, действующие совместно. Положим, что взаимодействие пульсаций, как и кажущаяся турбулентная вязкость, линейно зависят от координаты у и, соответственно, от безразмерной координаты ηу. Тогда доля времени существования профиля скорости, сформированного независимыми пульсациями, составляет σн = (ηy1 – ηy)/(ηy1 – ηy0), a доля времени существования профиля скорости, сформированного совместными пульсациями, составляет σс= 1– σн = (ηy – ηy0)/(ηy1 – ηy0). Выражение для осредненной скорости поперек переходного подслоя принимает вид:
U = σн (U1+U2)/2+ σс U. (19)
Подстановка вязкостей от обеих пульсаций с учетом указанных выше долей, а также частично объединенных пульсаций в уравнение (19) и последующее интегрирование уравнения (19) от ηy0 до ηy позволяют получить все поле скорости от стенки до внешней границы погранслоя. Поскольку окончательное выражение содержит слишком много слагаемых, представим это выражение в сокращенной форме:
φ = φ1+ φ2 = 1.25 (f/2)1/2 Re (C1/B1 + C2/B2), (20)
где
B1 = 0.099 [ηy1/( ηy1 – ηy0)] (f/2)-1/4Re3/4 – ηy0/( ηy1 – ηy0) (f/2)1/2 Re, (201)
В2 = 0.0221 [ηy1/( ηy1 – ηy0)]Re – ηy0/( ηy1 – ηy0) (f/2)1/2 Re, (202)
C1 = ln[η/(B1 + 0.0221/(ηy1 – ηy0) Re η]/{ηy0/[B1 + 0.0221 Reηy0/(ηy1 – ηy0)]}, (203)
C2 = ln(η/[B2 + 0.099(f/2)-1/4 Re3/4 η/( ηy1 – ηy0)]/{(ηy0/[B2 + 0.099(f/2)-1/4 Re3/4 ηy0/( ηy1 – ηy0)]}. (204)
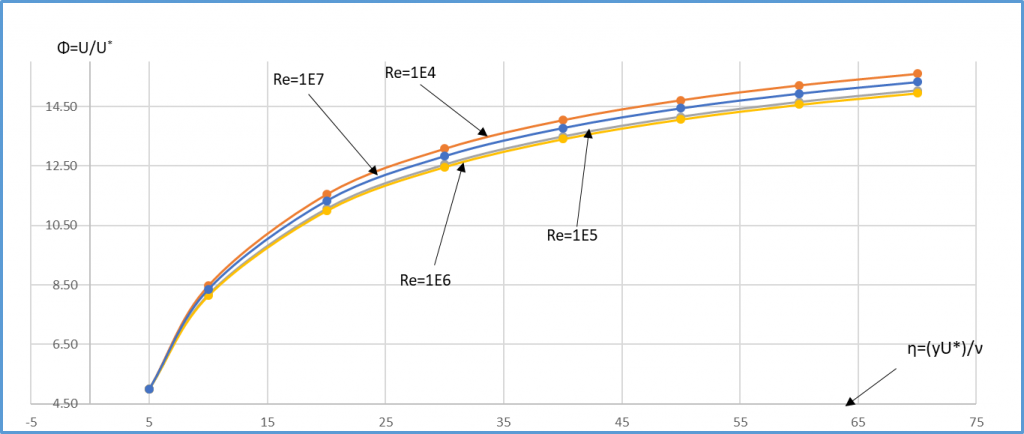
Автор приводит уравнения (20), как инструмент для дальнейшего изучения при оптимизации тепло- и массообмена. На рис. 1 пoказано поле скоростей турбулентного потока в диапазоне чисел Re от 104 до 107, рассчитанное по формуле (20) для переходного подслоя от ηy0 = 5 до ηy1 = 70. Кривая на рис. 1 хорошо совпадает с кривой, приводимой Шлихтингом в монографии [1]. Видно, что кривые на рис. 1, построенные для различных чисел Re, при приближении к внешней границе переходного слоя несколько отличаются друг от друга, но это отличие крайне невелико: соответствующее среднее стандартное отклонение составляет 1.5%, и максимальное отклонение нигде не превышает 2%. Это означает, что для проведения практических расчетов они могут быть аппроксимированы некоторой универсальной зависимостью вида j = j(h), которая может быть сопряжена с универсальным профилем Прандтля для ядра пограничного слоя.
Поле скоростей в ядре погранслоя
В режимах развитой турбулентности в трубах ядро включает большую часть пограничного слоя от внешней границы переходного подслоя у1 до внешней границы погранслоя d/2. Как следует из модели, в этой области оба типа пульсаций сливаются в одно целое, т. е. при расчете поля осредненных скоростей в ядре погранслоя можно пользоваться единой турбулентной вязкостью, рассчитанной как сумма двух компонентов:
νу = ν уδ1 + ν уδ2 = (y/ δ1) ν + (y/ δ2)ν. (21)
Подставляя в уравнение (21) значения δ1 и δ2, а также С1 = 25.3, В0 = 133 = 45.25*2.5, для сечения у внутри турбулентного ядра получим
νу = (y/d) ν [(f/2) -1/4 Re-3/4/C1 + Re/В0] = 0.4 (y/d) ν [0.099 (f/2)— 1/4 Re3/4 + 0.0221Re]. (22)
Выражение, приведенное в квадратных скобках, может быть заменено на (f/2) 1/2 Re в соответствии с уравнением (6). Отсюда:
νу = 0.4 (y/d) ν (f/2) 1/2 Re. (23)
Подставляя (23) в уравнение Буссинеска τ/ρ = νt (dU/dy), получим
где µ = νr — динамическая молекулярная вязкость жидкости.
Заменяя в уравнении (24) скорость U и координату у на безразмерные параметры φ и η, и интегрируя, приходим к уравнению Прантля:
φ = 2.5 ln(η) + 5.5, (25)
где φ — безразмерный параметр скорости, φ= U/U*.
Течение в трубах с песочной шероховатостью
Так же как и в гладкой трубе, течение жидкости в трубах с песочной шероховатостью хорошо изучено и описано в работах Никурадзе, Кармана, Прандтля и пр. При этом наибольшее влияние уделено режимам с полным проявлением шероховатости при безразмерном параметре расстояния от стенки ηш = (k U*)/ ν >70. Многочисленные эксперименты показывают, что при полном проявлении шероховатости, т. е. при значении ηш >70 фактор трения становится величиной постоянной, не зависящей от числа Re. Относительная шероховатость определяется, как ks = k/R, здесь k — высота элементов шероховатости (для песочной шероховатости — размер песчинок), R = d/2 — радиус трубы.
Для профиля скоростей при ηу > ηш в трубе с песочной шероховатостью по экспериментальным данным Никурадзе было получено уравнение [1]:
Φ = 2.5 ln(у/k) + 8.5. (26)
Уравнение (26) похоже на уравнение (25). Отличаются только выражения под знаком логарифма (уU*/ ν) в (25) и у/k в (26), и значения постоянных 5.5 в (25) и 8.5 в (26). Карманом [1] была получена формула для коэффициента сопротивления в шероховатой трубе:
f = [4*log(R/k) + 3.48]-2. (27)
Однако формула Прандтля f1/2 = [4lg(2 Ref1/2) – 1.6]-1 для расчета коэффициента сопротивления в гладкой трубе при высоких числах Re не согласуется с выражением (27). Чтобы доказать это, приравняем правые части обеих формул. Положим, что коэффициент k в выражении (31) достаточно мал, а число Re достаточно велико, что позволяет рассматривать шероховатую трубу, как гладкую. Тогда: 4*log (2 Re f ½) – 1.6 = 4*log (R/k) + 3.48, откуда Re f1/2 = 9.3 (R/k). Однако, если исходить из общепринятого и экспериментально подтвержденного понятия о том, что полное проявление шероховатости начинается от ηш = kU*/ν = 70, связь между числом Re и параметром шероховатости: Re f = 280 (R/k).
Чтобы устранить несоответствие уравнений Прандтля и Кармана, решение должно обеспечить соответствие обоих уравнений в области, где шероховатая труба становится гладкой, т. е. уравнение для расчета трения, учитывающее влияние шероховатости на сопротивление трубы, должно превращаться в уравнение (6), когда значение абсолютной k и относительной ks = k/R шероховатостей устремляются к 0. Такому условию отвечает, в частности, уравнение (6) для коэффициента трения в гладких трубах:
(f /2) ½ = 0.099 (f/2)-1/4 Re -1/4 + 0.0221.
В этом уравнении первое слагаемое в правой части представляет влияние пульсаций из ядра пограничного слоя, а второе слагаемое описывает пульсации, генерируемые в вязком подслое, и не зависящие от свойств поверхности. Таким образом, для коэффициента трения в шероховатой трубе можно записать:
(f /2) ½ = С (f/2)-1/4 Reкр-1/4 + 0.0221. (28)
Здесь С — постоянный коэффициент, определяемый из опытных данных, а Reкр — значение числа Re, при котором величина фактора трения для заданной шероховатости становится постоянной. Из опытов Никурадзе можно определить, что фактор трения f становится постоянным при числе Reкр, отвечающем условию (f/2) (k U*)/ν = 70, где высота шероховатостей k определяется из коэффициента относительной шероховатости k = ks d/2, и
Reкр = 140 ks-1 (f/2)-1. (29)
Подставив (29) в (28), получим:
(f /2) ½ = С/3.44 ks1/4 + 0.0221. (30)
Из опытных данных находим постоянную С = 0.427. Отсюда закон сопротивления для шероховатых труб выражается через число Re
(f /2) 1/2 = 0.427 (f/2)-1/4 Reкр -1/4 + 0.0221
или через относительную шероховатость
(f /2) ½ = 0.124 ks1/4 + 0.0221. (311)
Для получения профиля скоростей в трубе с шероховатой поверхностью используем тот же метод, что и для вычисления профиля скорости в гладкой трубе.
Как и для гладкой трубы, принимаем, что кажущаяся турбулентная вязкость по мере удаления от стенки линейно возрастает. Для турбулентной вязкости пульсаций с внутренним масштабом δ2, определяющих правое слагаемое в правой части уравнения (31), аналогично равенству (14) можно записать:
ν2у = (y/δ2) ν = 0.00884 (y/d) ν Reкр. (32)
Для турбулентной вязкости пульсаций с внутренним масштабом δ1 аналогично гладким трубам имеет место уравнение (13)
δ1/d = С1 (f/2) 1/4 Reкр-3/4, (33)
где С1 — константа.
Турбулентная вязкость пульсаций с внутренним масштабом δ1, аналогично турбулентной вязкости пульсаций из вязкого подслоя с внутренним масштабом δ2, определяется как νδ1 = ν, а турбулентная вязкость в сечении у1 равна
ν1y = (у1/d) ν (С1)-1 (f/2) -1/4 Reкр¾. (34)
Представленная здесь модель предполагает, что, как и в гладкой трубе, в вязком и переходном подслоях действуют пульсации обоих масштабов, которые объединяются в ядре турбулентного подслоя. Если в вязком подслое оба типа пульсаций действуют попеременно, то в переходном подслое они сливаются сначала частично, а к верхней границе — полностью. Поэтому в вязком подслое, где пульсации периодически сменяют одна другую, нужно рассматривать вязкость в каждом из полупериодов. Соответственно вязкость определяется следующим образом, начиная с верхней границы переходного подслоя у1:
νtу = ν1у + ν2у. (35)
Подставив в (35) компоненты турбулентной вязкости из (32) и (34), получим:
νty =0.4 ν (y/d) Reкр [(2.5/C1) (f/2) -1/4Reкр-1/4 + 0.0221ν]. (36)
Заменив теперь выражения в прямоугольных скобках на (f/2)1/2, из уравнения (31) получим:
νty = 0.4 ν (y/d) Reкр f1/2. (37)
Профиль скорости может быть найден из ранее приведенного выражения (18). После соответствующих подстановок (18) принимает вид:
Если переписать уравнение (38), добавив высоту шероховатостей k, получим общепринятую формулу
φ = 2.5 ln(у/k). (39)
Как уже указывалось, поскольку в вязком подслое оба типа пульсаций действуют попеременно, полностью сменяя друг друга, скорость потока, как и в гладкой трубе, определяется по среднему значению системой уравнений (17).
Для расчета профиля осредненной скорости в переходном подслое, как и для гладкой поверхности, нужно учитывать долю пульсаций масштабов δ1 и δ2, действующих независимо друг от друга, и долю пульсаций, действующих совместно.
Гладкая и шероховатая пластины
Поскольку методика, изложенная в настоящей работе, предполагается универсальной, ограничимся здесь только расчетными зависимостями для вычисления коэффициента трения. Для гладкой пластины:
(f /2)1/2 = 0.0255 (f/2)—1/2 Rex -1/4 + 0.0221.
Здесь f = f (x) — локальный коэффициент трения Rex = (Ux)/ν, x — расстояние от рассматриваемого сечения до передней кромки пластины. В диапазоне чисел Rex от 106 до 108 расхождение с опытными данными Вигхардта и Шлихтинга [1] не превышает 2%.
Для шероховатой пластины уравнение (40) принимает следующий вид:
(f /2)1/2 = 0.54 (f/2)—1/4 Rexкр -1/4 + 0.0221. (41)
Используя относительную шероховатость ks, как отношение высоты шероховатости k к длине х, получим:
(f /2)1/2 = 0.056 (f/2)—1/4 ks1/4 + 0.0221. (411)
Результаты расчетов по обеим формулам (41) и (411) хорошо совпадают как между собой, так и с опытными данными, а также с результатами расчета по интерполяционной формуле, приведенной в монографии Шлихтинга [1]: f = [2.87 – 1.58 log(ks)]-2.5.
Заключение
Сравнение зависимостей (6), (31), (40) и (41) для гладкой и шероховатой труб и для пластины показывает, что все зависимости выглядят подобно: во всех перечисленных уравнениях первые слагаемые в правой части характеризуют пульсации с внутренним масштабом δ1, генерируемые в ядре турбулентного подслоя. Во всех этих слагаемых содержится число Рейнольдса в степени -1/4, что является следствием потока диссипации в ядре погранслоя и следует закону ¾. Второе слагаемое во всех зависимостях — константа 0.0221, представляющая влияние пульсаций, генерируемых в вязком подслое. Можно назвать это слагаемое константой пристенной турбулентности. Все это подчеркивает возможность создания единой теории пристенной турбулентности для широкого поля поверхностей и геометрий на основе предлагаемой полуэмпирической модели с универсальными константами.
Автор выражает глубокую благодарность за ценные советы и редактирование к. т. н. М. Реузу и к. т. н. О. Маньковскому.
Литература
- Шлихтинг Г. Теория пограничного слоя. М., Наука, 1974.
- Лойцянский Л. Г. Механика жидкости и газа. М., Наука, 1973.
- Ландау Л. Д., Лифшиц Е. М. Теоретическая физика, т. 2. Гидродинамика. М., Гостехиздат, 1953.
- Левич В. Г., Физико-химическая гидродинамика. М., Физматгиз, 1959.
- Берман Я. А., Маньковский О. Н., Марр Ю. Н., Рафалович А. П. Системы охлаждения компрессорных установок. Л., Машиностроение, 1984.
- Деменок С. Л., Сивуха С. М., Медведев В. В. Визуализация течения жидкости в каналах. Страта, 2015.
- Репник Е. У., Соседко Ю. П. Турбулентный пограничный слой. М., Физматлит, 2007.
- Кутателадзе С. С. Основы теории теплообмена. М., Атомиздат, 1979.
Скачать PDF-файл статьи «Модель и полуэмпирический метод расчета пристенной турбулентности»