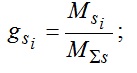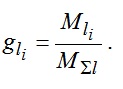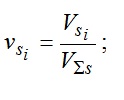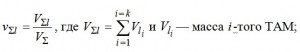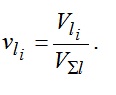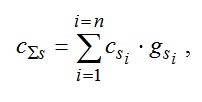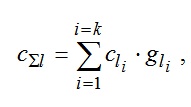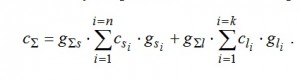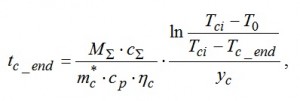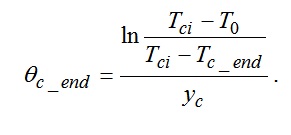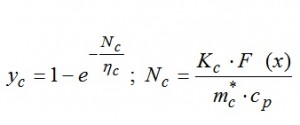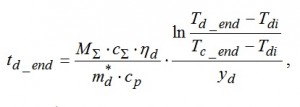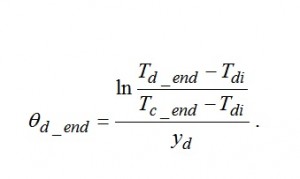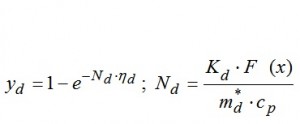Сайт научно-технического журнала «Инженерные системы. АВОК Северо-Запад»

Тепловые накопители в строительстве: учет применения нескольких теплоаккумулирующих материалов

Авторы:

Н. И. Ватин, директор Инженерно-строительного института СПбГПУ

М. И. Куколев, профессор кафедры «Гидравлика» Инженерно-строительного института СПбГПУ

В статье рассматриваются особенности применения нескольких теплоаккумулирующих материалов в одном тепловом накопителе, что нередко встречается на практике. Сочетания могут быть различными: несколько жидких однофазных материалов, несколько твердых материалов или жидкие и твердые одновременно. Определены массогабаритные и теплофизические характеристики устройства. Приведены зависимости для последовательного включения накопителя в тепловую систему.

Рис. 1. Расчетная схема матрицы теплового накопителя с однофазными
теплоаккумулирующими материалами

Повышение энергетической эффективности жилых и общественных зданий [1] напрямую связано с применением современного оборудования и, в частности, тепловых накопителей (ТН) энергии [2, 3]. На практике приходится сталкиваться с задачей оценки эффективности применения подобных систем, причем ее решение может осложняться одновременным применением нескольких теплоаккумулирующих материалов (ТАМ).

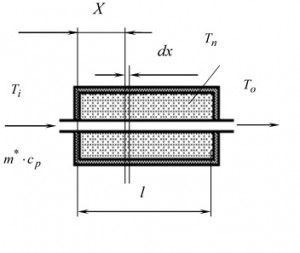
По аналогии с [4] рассмотрим расчетную схему плоской ячейки теплового накопителя последовательного включения с однофазным ТАМ (рис. 1). Вокруг канала с протекающим по нему теплоносителем тепловой системы расположены теплоаккумулирующие вещества. Массовый расход теплоносителя в канале m*, теплоемкость C_p— . При заряде температура теплоносителя на входе в накопитель  T_ci больше температуры на выходе из него T_co. Протекая по каналу и остывая, горячий теплоноситель отдает энергию ТАМ. Накопление энергии происходит за счет теплоемкости, температура материала T_n возрастает.

При разряде температура теплоносителя на входе в накопитель  T_di меньше температуры на выходе из него  T_do. Протекая по каналу, холодный теплоноситель нагревается за счет остывания ТАМ. Температура материала T_n понижается.

Пусть ячейка матрицы ТН состоит из n — твердых однофазных материалов и имеет заполнение  k— жидкими теплоаккумулирующими материалами. Общая масса матрицы M_Σ  складывается из суммарных масс ТАМ однофазных твердых M_Σs  и жидких M_Σi :

Определим массовые доли:

1) всех твердых ТАМ —

2) каждого из твердых ТАМ —

3) всех жидких ТАМ —

4) каждого из жидких ТАМ —

Объем матрицы V_Σ  складывается из суммы объемов однофазных твердых ТАМ V_Σs  и жидких  V_Σi — .

Определим объемные доли:

1) всех твердых ТАМ —

2) каждого из твердых ТАМ —

3) всех жидких ТАМ —

4)  каждого из жидких ТАМ —

Теплоемкость твердых ТАМ определится как:

где c_si — теплоемкость i -того твердого ТАМ.

Теплоемкость жидких ТАМ:

где c_li — теплоемкость i -того жидкого ТАМ.

Суммарная теплоемкость матрицы будет:

Каждый из ТАМ имеет некоторую критическую температуру T_kr . При ее достижении у жидких материалов начинается испарение с соответствующим возрастанием давления в ячейке, что может быть неприемлемым из конструктивных соображений. Твердые материалы при достижении критической температуры могут также разрушаться. Поэтому максимально достижимая температура нагрева матрицы из твердых и жидких ТАМ T_n = T_c_end будет определяться температурой T_kr  = T_kr_min — минимальной критической температурой из всех применяемых ТАМ, причем T_c_end < T_kr_min.

Если матрица нагревается от начальной температуры T_n = T_o до конечной температуры  T_n = T_c_end, то длительность этапа заряда ТН последовательного включения составит:

или в безразмерном виде:

Здесь η_c— энергетический КПД ТН при заряде;

— безразмерное число теплопередачи, где  K_c — коэффициент теплопередачи от теплоносителя к ТАМ и F(x)— площадь поверхности теплообмена.

Если от матрицы с начальной температурой T_n = T_c_end  и конечной температурой T_n = T_d_end отводится теплота, то длительность этапа разряда ТН последовательного включения составит:

или в безразмерном виде:

Здесь η_d  — энергетический КПД ТН при разряде;

— безразмерное число теплопередачи, где  K_d — коэффициент теплопередачи от ТАМ к теплоносителю в канале.

Зная безразмерные времена процессов заряда Θ_c_end  и разряда  Θ_d_end для ТН с несколькими ТАМ, далее проводят по соответствующим формулам расчет температур и эксергетических КПД системы [4].

Литература

1. Горшков А. С., Ватин Н. И., Рымкевич П. П. Реализация государственной программы повышения энергетической эффективности жилых и общественных зданий // Строительные материалы, оборудование, технологии XXI века, 2014. — № 1. — С. 39–46.
2. Бекман Г., Гилли П. Тепловое аккумулирование энергии. — М.: Мир, 1987. — 272 с.
3. Левенберг В. Д., Ткач М. Р., Гольстрем В. А. Аккумулирование тепла. — Киев: Тэхника, 1991. — 84 с.
4. Куколев М. И. Основы проектирования тепловых накопителей энергии. — Петрозаводск: Изд-во ПетрГУ, 2001. — 240 с.

Скачать статью  в pdf-формате: Тепловые накопители в строительстве: учет применения нескольких теплоаккумулирующих материалов