Сайт научно-технического журнала «Инженерные системы. АВОК Северо-Запад»

Локализованное дистанционное тепловое воздействие закрученной струей

Ю. Н. Марр, советник генерального директора АО «НПО «Тепломаш»

Воздушное отопление помещения тепловентиляторами (или охлаждение фанкойлами) охватывает своим воздействием все внутреннее пространство. Эти приборы всасывают воздух помещения, нагревают или охлаждают его и выпускают в виде струй. В пространстве помещения возникает глобальная циркуляция воздушных масс разомкнутого характера: прежде чем воздушные массы, выпущенные в струе прибора, снова попадут в спектр всасывания, они проделают длинный путь, полностью перемешиваясь.

На практике часто возникает необходимость создания локализованного в пространстве конвективного воздействия, например, обогрев только одного рабочего места или охлаждение ограниченной партии продуктов в незаполненном складе. Используемые для этих целей тепловентиляторы или фанкойлы точно так же работают по разомкнутому циклу. Выпущенная нагретая или охлажденная струя после контакта с намеченным объектом рассеивается в пространстве помещения, а на всасывание (т. е. и в теплообменник прибора) поступает воздух основного помещения (холодный или теплый). В результате тепловая (холодильная) мощность прибора становится наибольшей для заданных температурных условий. Ее остатки после воздействия полностью рассеиваются.

Эффективность локализованных конвективных воздействий можно повысить в замкнутом цикле посредством так называемого «дистанционного всасывания» [1]. Истекающая из сопла кольцевая закрученная струя экранирует образовавшийся внутри струи протяженный факел всасывания с уходящим во всасывающий патрубок потоком. Этим исключается бесполезное рассеяние отработанного тепла (холода). Устройство, реализующее конвективное воздействие с дистанционным всасыванием, отличается от описанных в [1] (например, по [2]) тем, что в воздушном тракте установлен теплообменник — воздухонагреватель или воздухоохладитель. В настоящей работе сделаны оценки эффективности локализованного конвективного теплового воздействия в замкнутом цикле на основе структуры дистанционного всасывания.

1. Факел всасывания формируется в пределах рециркуляционной зоны с обратными токами и отсасыванием [1]. Разрежение в зоне зависит от тангенциальной скорости, степени закрутки в сопле и интенсивности отсасывания. Разрежение убывает по длине зоны. При посадке факела на опорную поверхность (пол, стенка) вдоль оси симметрии образуется концентрированный вихрь смерчевого типа. Устойчивая длина свободного факела зависит от отношения расходов всасывания и струи на выходе из сопла G_вс/G_о. По [1] расчетная оценка длины имеет вид

L^̅_ф = L_ф / D_o ≈ 2w̅_o(1 + δ‵_прит – δ‵_вс),                 (1)

где δ‵_вс = G_вс/G_о; δ‵_прит = ΔG_прит/ G_о — относительное приращение притока к струе на длине зоны, обусловленное действием дополнительного разрежения, создаваемого всасывающим патрубком ΔР_вс; D_o — диаметр сопла; w̅_o = w_mo / u_o — характерный параметр крутки [3]; w_mo — максимальная тангенциальная скорость на выходе из сопла; u_o — осевая скорость струи на выходе из сопла,

При δ‵_вс →0 слагаемое δ‵_прит также стремится к нулю и факел всасывания мало отличается от области обратных токов рециркуляционной зоны. Длина зоны без отсасывания в зависимости от параметра крутки может достигать четырех диаметров сопла (при w̅_o = 2). Включение интенсивного отсасывания (δ‵_вс →1) укорачивает зону непосредственно через удаление из нее массы, но одновременно и удлиняет через дополнительный приток массы, который характеризуется в (1) слагаемым δ‵_прит, по оценке [1], порядка единицы. Таким образом, при δ‵_вс →1 длина факела составляет те же четыре диаметра сопла.

Предполагается [3], что разрежение в области рециркуляционной зоны, формирующее симметричный градиент давления, вызывает движение масс из окружающего пространства в поперечном направлении к струе. Подтекающие массы вливаются в струю. Характерно, что этот процесс не имеет ничего общего с эжекцией обычных затопленных струй, однако полный расход в струе, включающий присоединенные массы G_пс, определяют параметром, аналогичным коэффициенту эжекции, λ_пм = (G_о +G_пс)/G_о. Установлено [4], что наиболее интенсивное вливание в струю присоединенных масс происходит в диапазоне гидравлических длин x/d ≤ 5, т. е. в окрестности циркуляционной зоны, где и формируется наибольшее разрежение. За пределами этой области x/d > 5 темп поступления присоединенных масс заметно снижается.

Расход подсоса к корню струи для x/d ≤ 5 можно оценить по зависимости Д. Н. Ляховского, полученной на основе обобщения экспериментальных данных по закрученным струям еще в середине прошлого столетия (ссылка [90] в [4]):

ΔG̅ = 0,5Θ_л + 0,207(1 + Θ_л)(x/d).                (2)

В (2) параметр крутки Θ_л принят равным удвоенной величине параметра стандартного вида Θ = М/КR, который приближенно можно выразить через отношение тангенциальной и осевой скоростей Θ ≈ W/U, где М — поток момента количества движения струи; К — поток количества движения струи (осевой импульс); R — радиус сопла (устья). С учетом (2), λ_пм = 1 + ΔG̅.

При интенсивной крутке с Θ = 2,0 (Θ_л = 4) на длине зоны в четыре диаметра сопла (без отсасывания) расход присоединенной массы (λ_пм – 1) по выражению (2) составит 6,14 расхода струи. Таким образом, λ_пм = 7,14 для L̅_з = 4,0.

Это означает, что горловина сильно закрученной струи даже без отсасывания из зоны обратных токов превращается в протяженную структуру, индуцирующую интенсивное подтекание масс из окружающего пространства и встраивание их в саму структуру.

Отсасывание из зоны, как было показано, добавляет к λ_пм приблизительно еще один расход струи, и получается окончательно λ_пм ≈ 8,0. В свободной струе (не опертой на поперечную плоскость) подтекающие массы встраиваются в струю, получают свою долю вращательного и осевого движения (импульса), а ниже по течению за пределами зоны пополняются новыми подтекающими массами (правда, уже со значительно меньшей интенсивностью). В струе, опертой на плоскость концом всасывающего факела, поток присоединенной массы (около семи расходов струи при Θ = 2,0) отделяется от струи и растекается по плоскости опоры. Растекание масс вокруг нижней части горловины струи, ограниченной плоскостью, с одновременным подсасыванием по высоте струи формирует мощную кольцевую вторичную циркуляцию тороидального вида.

Для сравнения с незакрученными струями приведем величины коэффициентов эжекции. Свободная осесимметричная турбулентная струя (сплошная — не кольцевая) имеет λ_э = (0,38/ζ)(x/d), где ζ — коэффициент качества струи (практически в технических устройствах ζ не бывает больше 0,8 [5]). Принимая x/d = L̅_з = 4,0, получим всего лишь λ_э = 1,9. В данном случае гидравлическая длина x/d = 4,0 формально меньше начального участка «нормальной» осесимметричной струи L̅_нач/ос = 5,9. Однако сделанная оценка допустима, поскольку возмущения потока в технических устройствах обычно ликвидируют начальный участок. В результате расход присоединенной массы в сильно закрученных струях может до семи раз превышать расход эжектированных масс незакрученных осесимметричных струй

(λ_пм – 1)/( λ_э – 1) = (7,14 – 1)/(1,9 – 1) = 6,8.

Таким образом, сильно закрученная струя, посаженная концом циркуляционной зоны (или факела всасывания) на опорную плоскость, формирует в окружающем ее пространстве тороидальную структуру, в которой циркулирует 6–7-кратный расход струи.

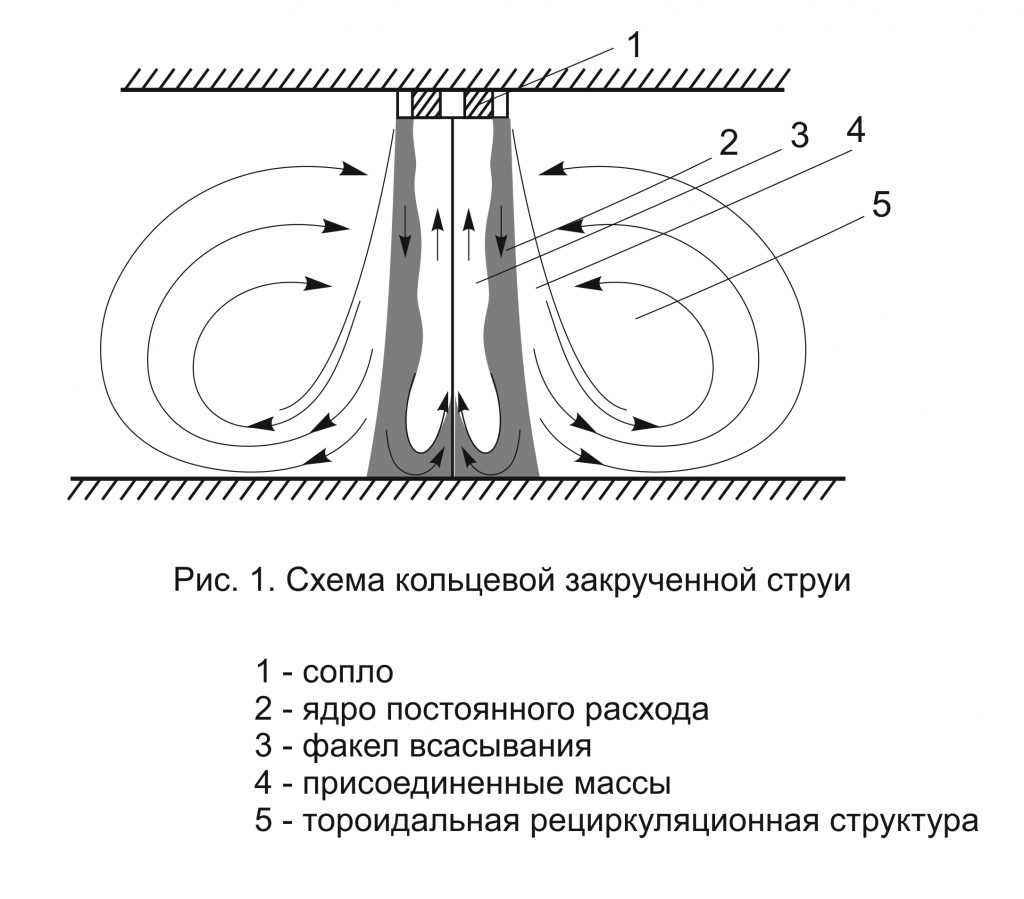
2. Схема такой вертикально ориентированной структуры показана на рис. 1. В ограниченном пространстве структура может оказаться сильно деформированной. Как было сказано, сильное разрежение закрепляет факел на стенке (на рис. 1 на полу), в нем возникает смерчевой вихрь и формируется сложная картина взаимодействия факела с окружающими и обтекающими его массами. Детали этой картины можно восстановить по экспериментальному изучению поведения вихревой нити в вихревой камере [6]. Разумеется, вихревая камера и рециркуляционная зона с факелом всасывания закрученной кольцевой струи — неидентичные объекты. Однако особенности взаимодействия вихревой нити с дном камеры могут оставаться аналогичными поведению смерчевого вихря в опертом на пол факеле всасывания.

Струя

Основная особенность этой структуры состоит в том, что резкое увеличение местной тангенциальной скорости с приближением к вихрю сопровождается таким же резким падением статического давления. В камере эпюры давления не меняются по высоте камеры и соответствуют значениям донного давления. По высоте свободного (не опертого на плоскость и без вихря) факела всасывания давление будет падать до максимального разрежения на срезе сопла. Однако после образования вихря возможно некоторое выравнивание разрежения по высоте факела с приближением донного давления к давлению во всасывающем патрубке.

Фотографии в [6] показывают, что вдали от дна камеры частицы жидкости двигаются по круговым траекториям, тогда как в донной области движение происходит по спиральным траекториям к центру. Это обусловлено образованием торцевого пограничного слоя при взаимодействии вихря с плоскостью. Это же приводит и к локализации завихренности в центральной части стенки и генерации из нее концентрированного вихря. Стягиваемые по стенке массы жидкости образуют интенсивный осевой поток вдоль вихря. В вихревой камере в этот поток переходит жидкость, поступающая в камеру из закручивающих сопел. В закрученной струе под действием вихря будут стягиваться не только массы из ядра постоянного расхода, но и массы обтекающего потока, поступающие через периферию области захвата.

Захват этих масс — наиболее сложная часть картины взаимодействия. Граница закрученной струи, упирающейся в пол, характеризуется противоположно направленными движениями. С одной стороны, часть ядра постоянного расхода вместе с присоединенными массами отсоединяется на некоторой высоте, где еще не действуют силы стягивания, и переходит в рециркуляционную структуру. С другой стороны, массы, окружающие струю и обтекающие ее по полу, попадают в область стягивания к центру и переходят в факел всасывания. Доля последних в общем расходе отсасывания, по-видимому, будет тем больше, чем относительно короче организован факел всасывания по отношению к его длине свободного состояния, т. е. чем сильнее будет разрежение на полу и интенсивнее стягивание масс к центру.

Согласно [2], область интенсивного захвата в факеле всасывания достигает 4–5 диаметров всасывающего патрубка. Это примерно соответствует рекомендованному в том же источнике соотношению: диаметр кольцевого сопла должен быть не менее чем в пять раз больше диаметра всасывающего патрубка. В [2] данная рекомендация преследует цель исключения неустойчивости вихря при взаимодействии близко протекающих противоположно направленных потоков и предотвращения его разрушения с выбросами за пределы факела всасывания. С другой стороны, рекомендация [2] совпадает с известной рекомендацией [6] диафрагмировать выход из вихревой камеры для получения устойчивого вихря.

3. Рассмотрим закрученную струю с внутренним дистанционным отсасыванием применительно к энергосберегающему тепловентилятору для локализованного теплового воздействия в пространстве. Энергосберегающий эффект такого тепловентилятора основан на использовании замкнутого цикла циркуляции, допускаемого дистанционным всасыванием. Полное отсасывание ядра постоянного расхода струи сформирует замкнутый цикл локализованного конвективного теплового воздействия на подстилающую поверхность и примыкающее к ней пространство. Этим исключается бесполезное рассеяние отработанного тепла (холода), как это происходит со струями обычных тепловентиляторов.

Различие температур струи и окружающего воздуха обусловит теплообмен между ядром постоянного расхода и присоединенными массами. Превалирующим механизмом теплопереноса будет турбулентный обмен молями. Растекающиеся по полу от факела присоединенные массы будут уносить и рассеивать перенесенную в них теплоту (или холод), а ядро струи, полностью (или большей своей частью) переходящее в факел всасывания, выйдет на заданный объект воздействия с соответствующей недостачей теплоты (или холода). Понятно, что даже с учетом затрат на собственно тепловое воздействие на заданный объект возвращающийся поток воздуха подойдет к теплообменному аппарату с температурой, отличающейся от окружающей среды. В этом и будет состоять экономия тепловой (холодильной) мощности замкнутого цикла в сравнении с разомкнутым.

4. Описанное в разделе 1 интенсивное движение в окружении струи наводит на мысль о возможном значительном уносе теплоты по длине струи, который ослабит предполагаемую экономию. Сделаем сравнительную оценку тепловой мощности, подводимой к приборам для локального обогрева выделенного объекта, при следующих заданных условиях:

• Расходы воздуха на выходе из прибора G_o = idem.
• Осевая скорость на выходе из сопла и из тепловентилятора v_o = idem.
• Температура окружающей среды t_a = idem.
• Температура струи, натекающей на объект воздействия, t_c = idem.
• Высота установки приборов над объектом H = 2,5d_o = idem.

Эффективность замкнутого цикла оценим отношением его тепловой мощности Q_зц к тепловой мощности обычного тепловентилятора Q_тв

Э = Q_зц / Q_тв.                            (3)

Для обычного тепловентилятора допустимо принять, что его струя целиком воздействует на заданный объект, полностью перемешивается. Это приводит к достаточному выравниванию температуры, так что температура t_c приблизительно равна среднемассовой в конце струи (далее теплоемкости опущены)

(G_o + G_э)t_c = G_o t_о + G_э t_а

или

(t_о – t_а) = λ_э(t_с – t_а)

Q_тв = λ_э G_o(t_с – t_а).                      (4)

В устройстве с дистанционным всасыванием, в силу отделения присоединенных масс, будем говорить о температуре струи t_с применительно к ядру постоянного расхода. При этом потери теплоты от ядра в присоединенные массы будут равны

ΔQ_пот1 = G_o(t_о – t_с) = Q̅_пот1G_o(t_о – t_а).          (5)

Здесь потери Q̅_пот1 представлены в форме, как в [5], а температура t_о отличается по величине от аналогичной температуры в (4).

Кроме потерь по выражению (5), следует учесть потери теплоты при воздействии струи непосредственно на объект

ΔQ_пот2 = G_o(t_с – t_вс),                      (6)

где t_вс — температура потока, уходящего по факелу всасывания в

теплообменный аппарат. Потери ΔQ_пот2 = a ΔQ_пот1 зададим для простоты как часть потерь ΔQ_пот1. Тепловая мощность устройства Q_зц равна сумме потерь

Q_зц = G_o(t_о – t_вс) = ΔQ_пот1 + ΔQ_пот2 = (1 + а) ΔQ_пот1.     (7)

Для использования (7) совместно с (5) в (3) необходимо температуру t_о выразить через t_с посредством (5)

t_о = ( t_с – Q̅_пот1 t_а)/(1 – Q̅_пот1),                (8)

откуда

Э = (1 + а) Q̅_пот1/ λ_э(1 – Q̅_пот1).              (9)

5. Сделаем оценку потерь Q̅_пот1 для кольцевой закрученной струи. Для этого воспользуемся приближенным методом расчета теплопотерь плоской струи в [5], дополнив его особенностями закрутки. Суть подхода в [5] состоит в том, что ядро постоянного массового расхода рассматривается как поток в воображаемом канале с проницаемыми стенками, обменивающийся теплотой с окружающей средой, омывающей канал организованными движениями эжектированных масс. В нашем случае омывать воображаемый канал будут присоединяющиеся массы. Введение воображаемого коэффициента теплоотдачи от ядра к окружающей среде позволяет записать обычное балансовое соотношение между текущей температурой ядра и теплопотерями через элемент площади воображаемого канала ядра. Далее это балансовое соотношение преобразуется в простейшее уравнение теории теплообменных аппаратов. После интегрирования в предположении постоянства коэффициента теплоотдачи по длине канала и ряда упрощений с аппроксимациями получено критериальное уравнение теплоотдачи в виде

St = 0,065(L/b_o)^–0,444,               (10)

где St = Nu/(RePr) — критерий Стантона; число Рейнольдса Re относится к потоку в воображаемом канале; L/b_o — гидравлическая длина струи (канала, ядра постоянного расхода). В (10) использованы данные по распределению температуры в поперечном сечении свободной затопленной плоской струи и по ширине ядра постоянного расхода. Непосредственно из (10) получается выражение для параметра, называемого в теории теплообменных аппаратов числом единиц переноса ε = αF/W_я

ε = 0,065 (L/b_o) ^0,556.            (11)

Для нагретой струи (t_o), разделяющей области с различными температурами (t₁ и t₂), получено выражение относительных потерь теплоты в сторону среды с температурой t₁ (здесь обозначения температур по [5])

Q̅_пот = 0,25(2 – θ₂)[1 – exp(–2ε)] + 0,5ε,     (12)

где Q̅_пот = Q_пот / (t_o – t₁) W_я; W_я = С_рG_я — водяной эквивалент ядра постоянного расхода; θ₂ = (t₂ – t₁)/(t_o – t₁). Рассмотрим возможности переноса результатов (10) – (12) на кольцевую закрученную струю.

Аэродинамическую картину наружной стороны тонкой кольцевой струи с параметром β = b_o/d_o ≤ 0,1, где b_o и d_o — ширина и диаметр кольцевого сопла, можно заменить плоской струей с начальной шириной b_o и с односторонней эжекцией. В этом случае выражение (12) может быть использовано для оценки теплопотерь прямоточной кольцевой струи. На внутренней стороне струи можно приближенно принять t₂ ≈ t_о, θ₂ ≈ 1 и упростить (12)

Q̅_пот = 0,25[1 – exp(–2ε)] + 0,5ε.     (13)

Выражения (10) – (13) получены с использованием экспериментальных результатов по распределению температур и скоростей в классических затопленных турбулентных струях, в которых процесс эжекции наружных масс осуществляется исключительно за счет естественного турбулентного переноса импульса. В закрученной струе в осредненном движении жидкость перемещается по раскручивающимся винтовым линиям тока. Наружные массы подтекают к струе под действием радиального градиента давления. Встречаясь на границе струи с вращающимися массами, они получают через хаотический перенос свою часть момента импульса и осевого импульса. Это сложное взаимодействие в плане аэродинамики можно интерпретировать как сильно интенсифицированное турбулентное движение. Из этого следует вывод, что полученные на естественном уровне турбулентности выражения (10) и (11) для условий закрученной струи дают заниженные значения теплопереноса. Невозможно дать строгую количественную оценку такой интенсификации турбулентности и теплопереноса. Однако качественная оценка может быть сделана на основе известных аналогов.

Например, при турбулентном течении в змеевике происходит интенсификация теплообмена за счет формирования вторичных течений, обусловленных искривлением канала. По различным расчетным зависимостям для змеевиков в многочисленной справочной литературе можно принять для развитого турбулентного режима (Re = 10⁴ – 10⁵) коэффициент интенсификации 1,5 по отношению к прямолинейной трубе. Если допустить возможность применения этой оценки к нашему случаю, то коэффициент в (11) заменяется с 0,065 на 0,1. Тогда, принимая гидравлическую длину струи L/b_o = (H/d_o)/ β = 2,5/0,1 = 25, имеем по (11) с коэффициентом 0,1 ε = 0,6, а тепловые потери от ядра постоянного расхода по (13) Q̅_пот = 0,475.

6. Для оценки коэффициента эжекции λ_э струи из тепловентилятора необходимо знать ее гидравлическую длину L̅_тв = L_тв/D_тв, где D_тв — эквивалентный гидравлический диаметр фронтального сечения тепловентилятора. Из равенства площадей выходных сечений приборов (равенство расходов и скоростей) найдем D_тв = 2d_о[(1 – β)β]^0,5, где β = b_o/d_o; b_o — ширина кольцевого сопла. Принимая β = 0,1 и учитывая, что L̅_з = 2,5, получим D_тв = 0,6d_о и L̅_тв =1,67 L̅_з = 1,67 х 2,5 = 4,2. Здесь предполагалось, что выходящая из тепловентилятора струя быстро становится осесимметричной. Полученная гидравлическая длина струи из тепловентилятора до объекта воздействия L̅_тв = 4,2 меньше длины начального участка «нормальной» осесимметричной струи L̅_нач/ос = 5,9. Однако струя из тепловентилятора не имеет отношения к «нормальным» струям: она вытекает из прямоугольного отверстия, загроможденного трубчато-ребристой теплопередающей поверхностью. Эпюра скорости достаточно неравномерна, поток сильно турбулизирован и возмущен жалюзийным устройством. Поэтому начальный участок практически отсутствует, коэффициент качества струи не превышает ζ = 0,6 [5], отсюда имеем λ_э = (0,38/0,6) L̅_тв = 2,66.

Принимая а = 0,3, получим по (9) коэффициент эффективности

Э = (1,3 х 0,475)/[2,66 х (1 – 0,475)] = 0,442

Как видно, прибор с дистанционным всасыванием (по замкнутому циклу) почти в два раза эффективнее обычного тепловентилятора при локализованном тепловом воздействии.

7. Примерная конструктивная схема устройства с дистанционным всасыванием может быть представлена следующим образом. Корпус располагается в верхней части помещения над объектом теплового воздействия. В центре корпуса расположено колесо радиального вентилятора, установленного на вертикальной оси электродвигателя. Колесо всасывает воздух через патрубок в нижней части корпуса из факела всасывания. Нагнетание колеса осуществляется в кольцевую камеру, из которой поток проходит через секции теплообменных аппаратов по периметру камеры. Получив теплоту (или холод), воздух поступает в кольцевое устройство с поворотом потока на 90⁰, с закручивающими лопатками и выходным соплом.

Выводы

Устройство с дистанционным всасыванием для конвективного теплового воздействия на локализованный в пространстве объект позволяет в два раза уменьшить затраты тепловой мощности в сравнении с обычным тепловентилятором (фанкойлом).

Литература

1. Марр Ю. Н. Дистанционное всасывание в технических приложениях// Инженерные системы. АВОК — Северо-Запад. № 1. 2022. С. 6–12.
2. Способ локальной вытяжной вентиляции и устройство для его осуществления. Патент RU Подача заявки: 2009.12.08. Опубликовано: 2011.09.10.
3. Теория турбулентных струй / Абрамович Г. Н., Гиршович Т. А., Крашенинников С. Ю., Секундов А. Н., Смирнова И. П. Изд. 2-е, перераб. и доп./Под ред. Г. Н. Абрамовича. — М.: Наука. 1984. 720 с.
4. Аэродинамика закрученной струи. Под ред. Р. Б. Ахмедова. М.: Энергия, 1977. 240 с.
5. Марр Ю.Н. Воздушно-тепловые завесы. Расчет и проектирование завес для защиты проемов промышленных и общественных зданий. СПб.: АО «НПО «Тепломаш». 2017. 160 с.
6. Алексеенко С. В., Куйбин П. А., Окулов В. Л. Введение в теорию концентрированных вихрей. Москва-Ижевск. Институт компьютерных исследований. 2005. 504 с.

Скачать PDF-версию статьи «Локализованное дистанционное тепловое воздействие закрученной струей»