Сегодня, 27 февраля
- (Нет мероприятий)
Ближайшие мероприятия
-
10 марта - 12 марта
-
12 марта / 10:00 - 13:30
-
20 марта - 22 мартаСанкт-ПетербургВыставка «Строим загородный дом»
-
24 марта - 26 марта
-
31 марта - 03 апреляМоскваВыставка MosBuild 2026
-
13 апреля - 17 апреляСанкт-ПетербургВсероссийский жилищный конгресс 2026
Защита проемов удаленными от створа импульсными струйными источниками
Ю. Н. Марр, советник генерального директора АО «НПО «Тепломаш»
В рамках традиционной струйной шиберующей защиты проемов рекомендуется размещать завесы в непосредственной близости створа проема, чтобы между вытекающими из сопел струями и краями проема не возникали промежутки, через которые наружный воздух мог бы затекать внутрь помещения. Реальные строительные конструкции вблизи проемов зачастую не позволяют устанавливать завесы в соответствии с проектными рекомендациями. К этому добавляются современные складные, подъемные и сворачивающиеся перекрытия ворот. Приходится отодвигать завесы от проема вглубь помещения, иногда на значительные расстояния. Однако, в общем случае, если не менять концепцию защиты, то в плоскости проема и в самой защитной струйной структуре возникают бреши для прохода наружного воздуха.
Первой попыткой организации защиты отодвинутыми от проема завесами, по-видимому, можно считать схему экранированной струи [1]. При всей необычности, схема экранированной струи не выходит за рамки традиционной концепции защиты. Это обстоятельство и отразилось в том, что наряду с повышением эффективности экранированные струи обладают существенным недостатком — они требуют значительного увеличения высоты помещения.
Изменение концепции защиты проема можно рассматривать в двух аспектах. Во-первых, переход от защиты проема боковой стороной струи к прямому лобовому противодействию. И, во-вторых, возврат к противодействию боковой стороной струи, однако с имитацией защиты нижней струей. В обоих случаях источник струи должен быть удален от проема.
В настоящей работе сформулированы основные принципы организации защиты проемов удаленными от створа импульсными струйными источниками.
Для понимания основных особенностей лобового противодействия струи затеканию наружных масс в проем рассмотрим классическую задачу о распространении турбулентной струи во встречном потоке. Такая задача решена в [2] приближенным интегральным методом. Струя вытекает из сопла диаметром 2δо со скоростью uo навстречу безграничному потоку со скоростью U∞. Формируется структура, ограниченная поверхностью, на которой продольные скорости равны нулю. На этой поверхности скорости направлены перпендикулярно оси симметрии. Ее охватывает другая поверхность — граница циркуляционной зоны. Внутри границы зоны развивается встречное движение струи, разворот потоков и спутное возвратное движение. Для наших целей необходима информация о зависимости длины циркуляционной зоны L и ее максимального диаметра D от соотношения скоростей m = U∞ /uo (см. табл. 1).
Таблица 1. Размеры циркуляционной зоны, образованной осесимметричной струей во встречном потоке по [2]
| m | 0,1 | 0,2 | 0,3 | 0,4 |
| L/2 δо | 36 | 20 | 14 | 11 |
| D/2 δо | 11 | 6 | 5 | 4,5 |
| L/D | 3,3 | 3,3 | 2,8 | 2,4 |
 В [2] показано, что решение хорошо согласуется с опытными данными, за исключением области критической точки. В табл. 1 приведены результаты, взятые с графиков [2]. Прямой перенос схемы с циркуляционной зоной [2] на случай защиты проема удаленным импульсным источником невозможен по той причине, что встречный поток неограничен и омывает циркуляционную зону со всех сторон, тогда как в нашей задаче струя первоначально остается свободной затопленной, а противодавление струе создается лишь в самом конце ее в области проема, где и формируется пятно взаимодействия. Тем не менее имеется возможность сделать оценку отношения расстояния от источника струи до воображаемого пятна взаимодействия (до критической точки) к диаметру пятна L/D. Как видно из табл. 1, при малых m это отношение равно 3,3. С ростом m (с увеличением разности давлений в проеме) отношение L/D убывает.
В [2] показано, что решение хорошо согласуется с опытными данными, за исключением области критической точки. В табл. 1 приведены результаты, взятые с графиков [2]. Прямой перенос схемы с циркуляционной зоной [2] на случай защиты проема удаленным импульсным источником невозможен по той причине, что встречный поток неограничен и омывает циркуляционную зону со всех сторон, тогда как в нашей задаче струя первоначально остается свободной затопленной, а противодавление струе создается лишь в самом конце ее в области проема, где и формируется пятно взаимодействия. Тем не менее имеется возможность сделать оценку отношения расстояния от источника струи до воображаемого пятна взаимодействия (до критической точки) к диаметру пятна L/D. Как видно из табл. 1, при малых m это отношение равно 3,3. С ростом m (с увеличением разности давлений в проеме) отношение L/D убывает.
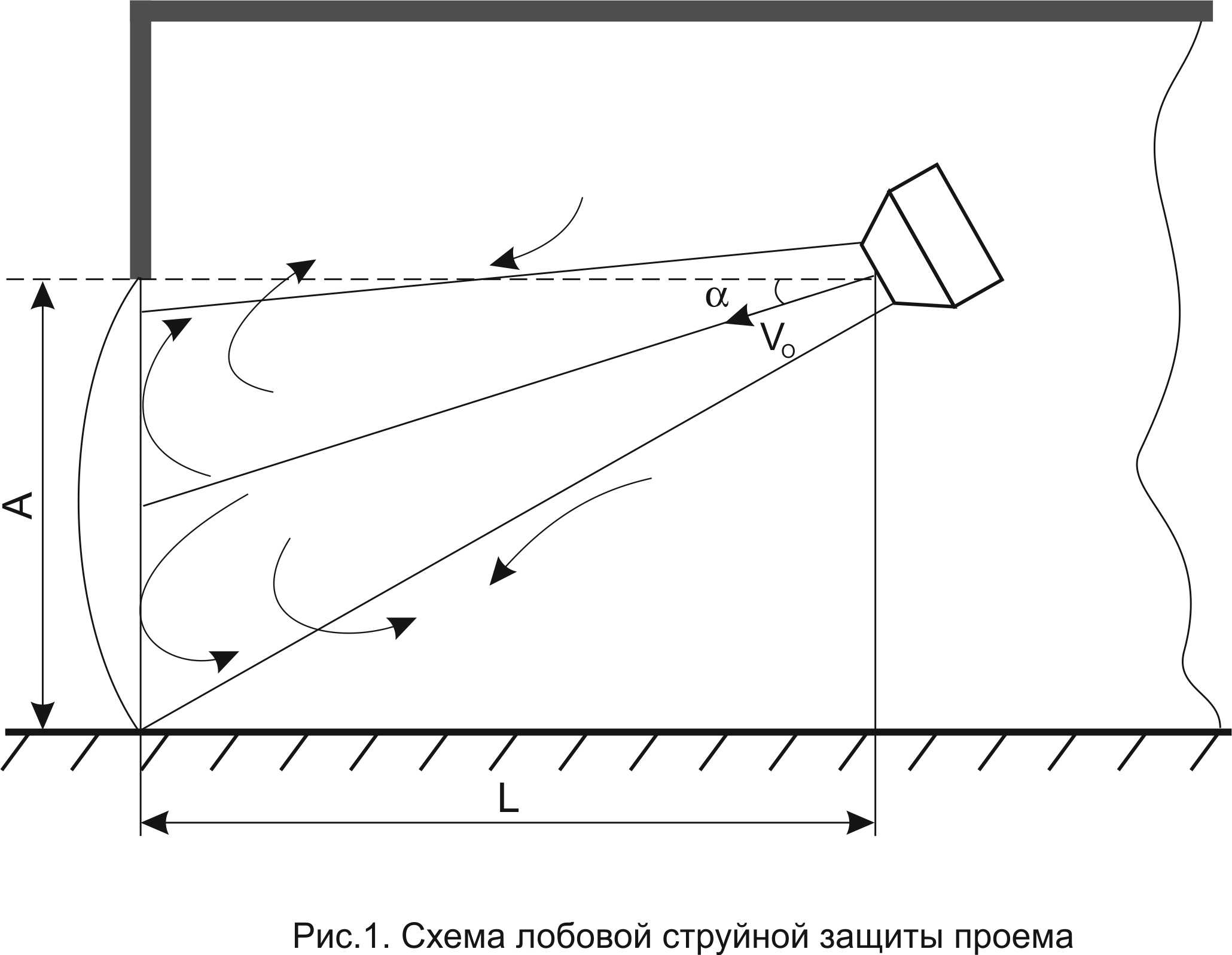
Рассмотрим оценку прямой импульсной защиты квадратного проема со стороной А. Пусть осесимметричный импульсный источник с диаметром сопла dо располагается на высоте (А + Δh) на расстоянии L от проема (рис. 1). Ось струи направлена в центр проема под углом α к нормали к проему. Здесь предполагается, что струя даже частично не отражается от пятна взаимодействия, а растекается по плоскости, на которой расположен проем. Поэтому давление струи в сечении взаимодействия определяется потоком импульса струи с учетом угла набегания. Используя известные приближенные зависимости скоростей и расходов струи для осесимметричного источника, например, по [1]:
скорость на оси основного участка ‹vm›/vo = 5,9/(z/do),
коэффициент эжекции λос = Gс/Gо = 0,34(z/dо), (1)
среднеквадратичная скорость струи vср/‹vm› = 0,48= const,
найдем связь между площадью сечения струи вблизи проема Fcи длиной траектории струи Lc:
F̅c = 0,12 L̅2c, (2)
где F̅c = Fc/Fо, L̅c= Lc/do, Fc = Gс/ρ vср, Fо = π do2/4, vср — среднемассовая скорость.
Из условия постоянства потока импульса давление струи на плоскость проема равно
Р̅с F̅c = cos2α, (3)
где Р̅с = Рc/ρ vo2.
Далее принято первое условие защиты, состоящее в том, что давление струи на плоскость проема равно средней расчетной разности давлений в проеме Рc = Δ Рпр. Второе условие заключается в равенстве площадей пятна взаимодействия и проема
А̅ 2 = F̅c / cosα. (4)
Из схемы рис. 2 следует соотношение
L̅c2 = L̅2+ Н̅ 2, (5)
где
Н̅ = 0,5А̅ + 0,5 + h̅, (6)
черточка над буквой означает отнесение к диаметру do.
Угол между осью струи и нормалью к плоскости проема определяется выражением
α = arctg(H̅/L̅). (7)
Введя переменную x = L̅/H̅ и преобразовывая уравнения (2) – (7), получим расчетное уравнение для определения переменной х методом последовательных приближений
х = [10,6 А̅ 2 arctg(1/x)/ Н̅ 2 – 1]0,5. (8)
Далее определяются величины L̅, α, Δ Р̅пр по выражению (3) с учетом (2) и (5)
Δ Р̅пр = 8,33 cos2α/(L̅2+ Н̅ 2 ), (9)
скорость струи
vo = (Δ Рпр/ρ Δ Р̅пр)0,5, (10)
расход источника (вентилятора) Vo = vo Fо. Эквивалентная величина параметра m равна
m = (2 ΔР̅пр)0,5. (11)
 Расчеты по выражениям (2) – (11) для двух значений размеров проема представлены в табл. 2. Мощность вентилятора определялась по коэффициенту расхода сопла 0,8 и КПД вентилятора 0,7. Размер h = 0, диаметр сопла принят do = 0,8 м.
Расчеты по выражениям (2) – (11) для двух значений размеров проема представлены в табл. 2. Мощность вентилятора определялась по коэффициенту расхода сопла 0,8 и КПД вентилятора 0,7. Размер h = 0, диаметр сопла принят do = 0,8 м.
Как видно, требуемое данной схемой удаление вентилятора от плоскости проема вглубь помещения составляет около трех высот проема (L/А). Увеличение вдвое высоты и ширины проема (площади проема в 4 раза) приводит к почти трехкратному росту расхода воздуха и более чем двадцатикратному росту мощности вентилятора. Это означает, что для защиты проемов больших размеров целесообразно переходить на более крупные вентиляторы. При всей условности сопоставления результатов табл. 1 и 2 можно видеть качественное совпадение отношений L/А и L/D в зависимости от m.
Таблица 2. Параметры защиты проема удаленным импульсным источником
| А, м // А̅ | 3 // 3,75 | 6 // 7,5 |
| ΔРпр, Па(принято) | 4,0 | 8,0 |
| L̅ // L, м | 11,9 // 9,5 | 23,8 // 19,1 |
| α, град | 11,3 | 10,1 |
| ΔР̅пр | 0,0544 | 0,0138 |
| vo, м/с | 7,8 | 22,0 |
| m | 0,33 | 0,17 |
| L/А | 3,2 | 2,5 |
| Vо, м3/час | 14 040 | 39 540 |
| Nвент, кВт | 0,32 | 7,1 |
В рамках принятой схемы проследим влияние диаметра вентилятора (точнее, диаметра сопла источника). Размер проема А = 3 м, расположение вентилятора, по-прежнему, над верхней кромкой проема h = 0. Расчеты сведены в табл. 3.
Таблица 3. Влияние диаметра сопла на защитную конфигурацию
| do, м | 1,0 | 0,8 | 0,6 | 0,5 |
| А̅ | 3,0 | 3,75 | 5,0 | 6,0 |
| Н̅ | 2,0 | 2,38 | 3,0 | 3,5 |
| L̅ // L, м | 9,45 // 9,45 | 11,9 // 9,48 | 15,9 // 9,50 | 19,1 // 9,53 |
| α, град | 12,0 | 11,3 | 10,7 | 10,4 |
| ΔР̅пр | 0,0854 | 0,0544 | 0,0309 | 0,0215 |
| vo, м/с | 6,3 | 7,8 | 10,4 | 12,5 |
| Vвент, м3/час | 17 813 | 14 114 | 10 585 | 8836 |
| Nвент, кВт | 0,27 | 0,32 | 0,43 | 0,52 |
Независимо от диаметра сопла защитная конфигурация остается неизменной: расчетное удаление вентилятора от плоскости проема сохраняет свою величину 9,5 м. Это и понятно: из (2) следует, что заданная абсолютная площадь сечения осесимметричной струи определяет расстояние этого сечения от сопла. Если при прочих равных условиях источник расположить дальше, то площадь сечения струи вблизи проема станет больше, соответственно, давление струи меньше и в рамках данной схемы возникнет затекание наружного воздуха в проем. Напротив, если источник окажется ближе, то площадь пятна взаимодействия будет меньше площади проема, а давление на пятне больше. При этом произойдет как минимум частичное вытекание струи наружу и затекание наружных масс в проем по периферии.
 Направление струи в центр проема или при широком проеме в центры частей проема создает определенные затруднения в реализации данной схемы. В таких сложных течениях, как плотная система параллельных струй с регулярными разворотами, устойчивая структура маловероятна. Скорее всего, смыкающиеся по бокам струи еще на подходе к проему переформировываются в структуру, аналогичную плоской струе. Но у плоского потока, набегающего на открытый проем со сбалансированным противодавлением, имеется лишь одна степень свободы — преимущественный разворот вверх и возврат на всасывание вентиляторов в общей циркуляции. Даже такая упрощенная интерпретация аэродинамической картины вызывает ассоциацию с защитой проема нижней завесой. Известно, что нижние завесы являются наиболее эффективным способом защиты проемов, однако их реализация приводит к существенному усложнению и удорожанию архитектурно-строительных конструкций.
Направление струи в центр проема или при широком проеме в центры частей проема создает определенные затруднения в реализации данной схемы. В таких сложных течениях, как плотная система параллельных струй с регулярными разворотами, устойчивая структура маловероятна. Скорее всего, смыкающиеся по бокам струи еще на подходе к проему переформировываются в структуру, аналогичную плоской струе. Но у плоского потока, набегающего на открытый проем со сбалансированным противодавлением, имеется лишь одна степень свободы — преимущественный разворот вверх и возврат на всасывание вентиляторов в общей циркуляции. Даже такая упрощенная интерпретация аэродинамической картины вызывает ассоциацию с защитой проема нижней завесой. Известно, что нижние завесы являются наиболее эффективным способом защиты проемов, однако их реализация приводит к существенному усложнению и удорожанию архитектурно-строительных конструкций.
Покажем, что посредством удаленных импульсных источников возможна эффективная имитация защиты нижней завесой. Возьмем за основу следующую схему. Струя от источника, расположенного выше верхнего створа проема, направлена под углом к проему и ударяет в пол на некотором удалении от проема. В результате соударения формируется стелящаяся струя, направленная на проем. Противодавление отрывает струю от пола и разворачивает струйные массы в противоположном направлении. Параметры течения должны быть таковы, чтобы поперечные размеры разворота полностью перекрывали проем и противодействовали втеканию наружных масс.
Предлагаемая схема опирается на экспериментально полученную картину: соударение осесимметричной турбулентной затопленной струи с плоским экраном под некоторым углом в условиях неограниченного внешнего потока, направленного навстречу струе (рис. 8.4.1 в [3]). Показано что струя, стелящаяся вдоль поверхности навстречу потоку, отрывается, образуя зоны разворота и обратного распространения струи. Внешний поток также отрывается, обтекая зоны разворота струи. В целом образуется вихревая зона. Ориентировочно относительные размеры вихревой зоны (отнесенные к диаметру сопла) при угле струи 450, относительном напоре 0,01 и относительной высоте сопла над экраном 6 равны: высота 10, протяженность от зоны соударения 20, ширина в сечении зоны соударения 17. Соотношение продольного и поперечного масштабов структуры равно 20/10 = 2.
 Рассмотрим возможное развитие защитной структуры проема, имитирующей нижнюю завесу. С этой целью воспользуемся приложением уравнения импульсов к струе по аналогии с работой [4], в которой получено решение для односторонней боковой завесы. В [4] рассматривается действие потоков импульса и сил на текущий контур, связанный с точкой А, расположенной на оси струи. В соответствии со схемой для односторонней боковой завесы разность давлений вдоль размаха проема в [4] принята постоянной. Интегрирование дифференциального уравнения импульсов для текущего контура с перемещаемой по траектории точкой А приводит к уравнению траектории струи. Используя выражения для проекций скоростей, можно показать, что модуль потока импульса вдоль траектории струи сохраняется. Струю при этом можно рассматривать как свободную затопленную по аналогии с [5]. В схеме по [4] использованы значительные упрощения действительной картины течения. Так, реальная струя конечной толщины с конечным расходом и потоком импульса сведена к линии (траектории, оси струи), при этом давление в проеме меняется скачком на оси струи, тогда как в свободной струе давление остается неизменным в поперечном сечении струи. Тем не менее схема [4] с корректировкой по [1] дает не только качественное, но и количественное удовлетворительное совпадение с расчетными рекомендациями [6], опирающимися на экспериментальные данные.
Рассмотрим возможное развитие защитной структуры проема, имитирующей нижнюю завесу. С этой целью воспользуемся приложением уравнения импульсов к струе по аналогии с работой [4], в которой получено решение для односторонней боковой завесы. В [4] рассматривается действие потоков импульса и сил на текущий контур, связанный с точкой А, расположенной на оси струи. В соответствии со схемой для односторонней боковой завесы разность давлений вдоль размаха проема в [4] принята постоянной. Интегрирование дифференциального уравнения импульсов для текущего контура с перемещаемой по траектории точкой А приводит к уравнению траектории струи. Используя выражения для проекций скоростей, можно показать, что модуль потока импульса вдоль траектории струи сохраняется. Струю при этом можно рассматривать как свободную затопленную по аналогии с [5]. В схеме по [4] использованы значительные упрощения действительной картины течения. Так, реальная струя конечной толщины с конечным расходом и потоком импульса сведена к линии (траектории, оси струи), при этом давление в проеме меняется скачком на оси струи, тогда как в свободной струе давление остается неизменным в поперечном сечении струи. Тем не менее схема [4] с корректировкой по [1] дает не только качественное, но и количественное удовлетворительное совпадение с расчетными рекомендациями [6], опирающимися на экспериментальные данные.
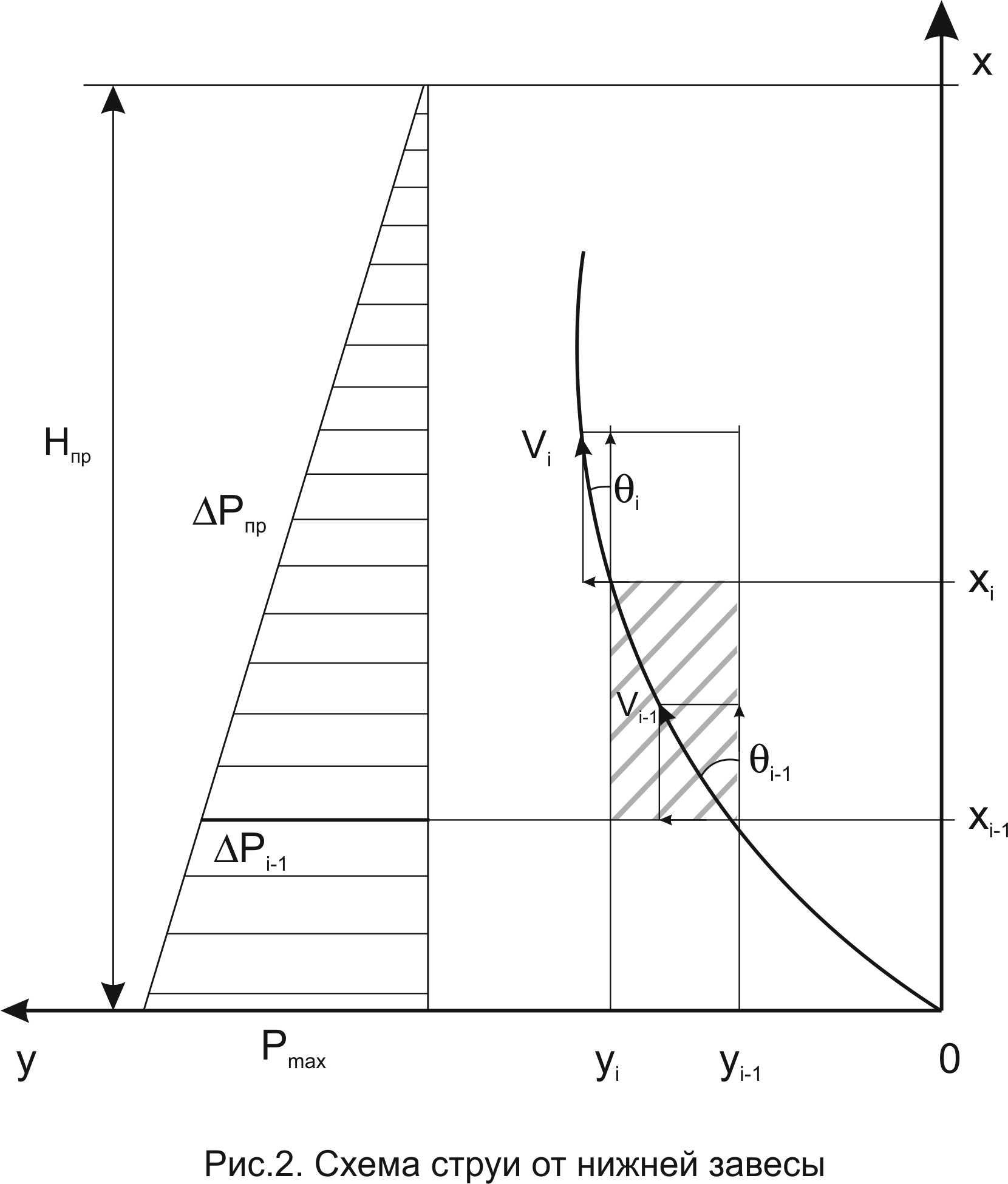
В отличие от [4], где разность давлений ΔРпр в любой точке траектории постоянна, в нашем случае при перемещении точки А снизу вверх гравитационное давление меняется от максимального на нулевой отметке Рн = gΔρНпр = Рmaxдо нуля на уровне верхнего створа проема (имея в виду герметичное помещение). Схема течения струи от нижней завесы представлена на рис. 2. Примем линейный закон изменения гравитационного давления по высоте проема
ΔРпр = Рmax(1 – х/Н). (12)
Для дальнейшего разобьем всю траекторию на n участков и применим уравнение импульсов по аналогии с [4] к каждому участку (здесь всюду используется среднемассовая скорость). Тогда, в соответствии с уравнениями по [4], для i-того участка можно записать составляющие скорости
vy = [ρbi-1v i-12sinθi-1 – (x – xi-1)ΔPi-1]/ρbv (13)
vx = [ρbi-1v i-12cosθi-1 + (y – yi-1)ΔPi-1]/ρbv, (14)
где индексом i-1 отмечены параметры входа струи в контрольный объем i-того участка, без индекса — текущие параметры внутри участка, b — ширина струи (по среднемассовой скорости), θ — угол между вектором скорости и осью х.
Тангенс угла наклона траектории в текущей точке равен
tgθ = dy/dx = vy /vx = [ρbi-1v i-12sinθi-1 – (x – xi-1)ΔPi-1]/[ρbi-1v i-12cosθi-1 + (y – yi-1)ΔPi-1]. (15)
Введем упрощения. Будем считать, что струя вдоль траектории распространяется с постоянной скоростью, равной скорости на входе на траекторию vо, и ширина струи также
не изменяется и равна bо. Здесь принято, что ширина стелящейся струи bо совпадает с
шириной свободной струи от удаленного источника в непосредственной близости от пола. В соответствии с зависимостями для плоской струи [1], независимо от ширины сопла удаленного источника (завесы), ширина свободной струи равна bо = (0,55ξ)2Lстр = 0,476 Lстр (при ξ = 0,8), где Lстр — длина струи от источника до сечения разворота струи и перехода в стелящуюся (в расчетах принято, что Lстр ограничена плоскостью, отстоящей от пола на высоту bо/2.
Преобразуем (15) к виду
tgθ = [sinθi-1 – (xˉ – xˉi-1)εi-1]/[cosθi-1 + (yˉ – yˉi-1) εi-1], (16)
где εi-1 = ΔPi-1 / ρv о2, xˉ = x/bо, yˉ = y/bо. Тангенс угла наклона в конце i-того участка равен
tgθi = [sinθi-1 – (xˉi – xˉi-1)εi-1]/[cosθi-1 + (yˉi – yˉi-1)εi-1].
Для упрощения заменим плавную траекторию ломаной линией, состоящей из n участков с одинаковой длиной Δl и углами наклона θi-1. Тогда будем иметь (xˉi – xˉi-1) = Δlˉcos θi-1, (yˉi – yˉi-1) = Δlˉ sin θi-1 и далее
tgθi = [sinθi-1 – εi-1 Δlˉcos θi-1]/[cosθi-1 + εi-1 Δlˉ sin θi-1]
или
tgθi = tgθi-1[1 – (εi-1 Δlˉ)/tgθi-1]/[1 + (εi-1 Δlˉ) tgθi-1]. (17)
Используя (12), зададим расчетный дискретный ряд εi-1 от xˉо = 0 до xˉ = Нпр/ bо:
i-1
εi-1 = εmax[1 – (bо./ Hпр)( ΔlˉΣ cos θj )]. (18)
j=0
В (18) εmax = ΔPmax / ρv о2. Поперечная координата оси струи равна
i-1
yˉi = ΔlˉΣ sin θj. (19)
j=0
По выражениям (17) – (19) приближенно рассчитывается траектория струи в поле переменной разности давлений в проеме. В начальной точке траектории положим
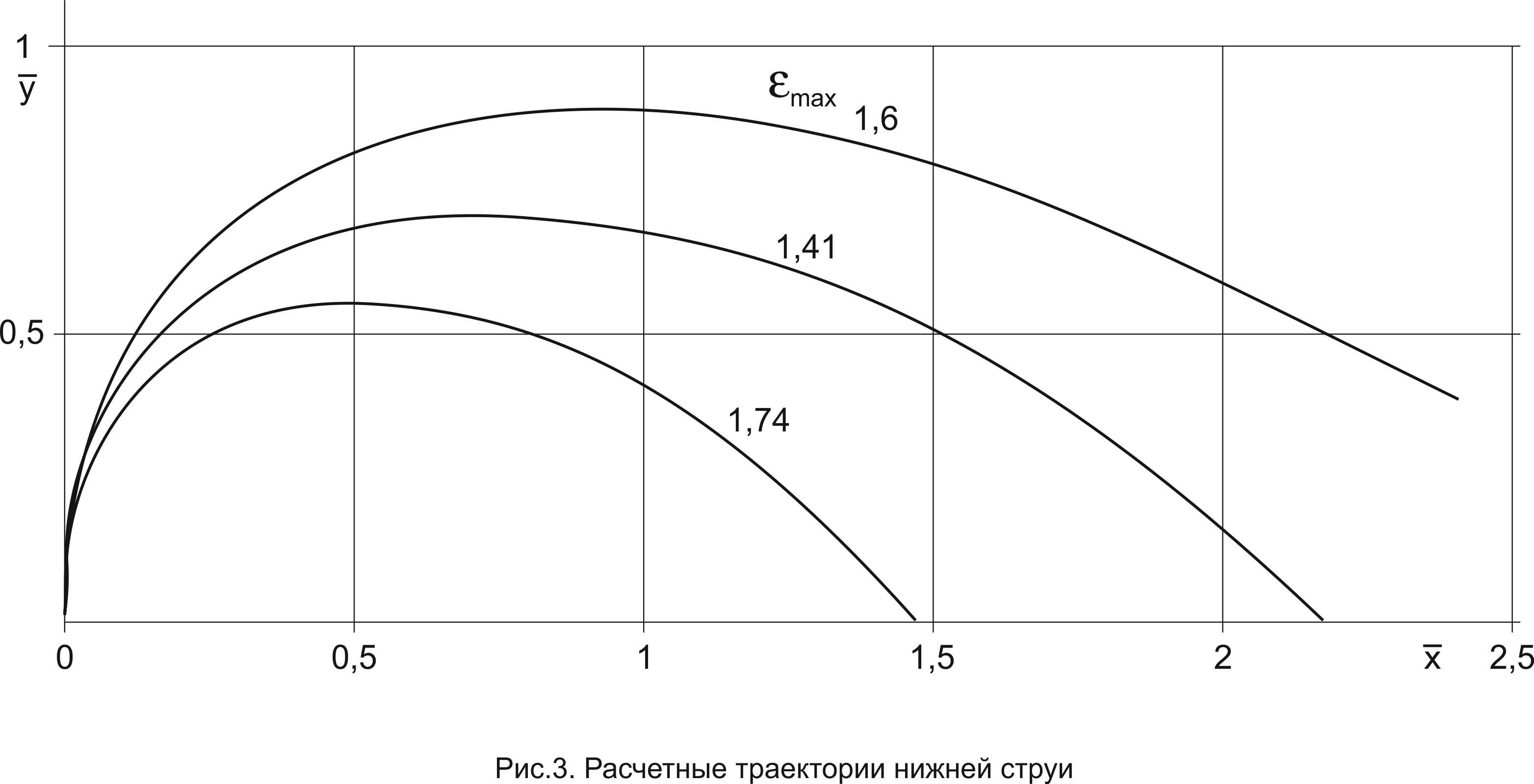
θi-1 = 900. При этом выражение (17) превращается в неопределенность, после разрешения которой получаем tgθ1 = 1/ε1 Δlˉ. Результаты расчетов нескольких вариантов приведены на рис. 3 для следующих условий:
— температура воздуха — наружная –35 0С, внутренняя +18 0С, Δρ = 0,27 кг/м3,
— помещение герметичного типа,
— высота проема 16 м,
— максимальная разность гравитационных давлений Рmax= 42,3 Па,
— высота середины выходного сечения сопла источника 16 м, угол струи к полу 110, расчетная длина струи 13,4 м, начальная ширина струи, стелящейся по полу, bо = 6,4 м,
— длина i-того участка Δl = 1 м, соответственно, Δlˉ = 0,16,
— гидравлическая высота проема Hпр/bо = 2,5.
Варьируя скорость струи v о в диапазоне от 4 до 5,5 м/с, были рассчитаны три варианта струй с осевыми линиями (траекториями), представленными на рис. 3 в зависимости от параметра εmax. Как видно, при самой высокой скорости 5,5 м/с (εmax = 1,16) струя оказывается настолько избыточно мощной, что уходит за пределы проема. При скорости 4,5 м/с (εmax = 1,74) разность давлений заставляет затекать струю в проем в режиме неполной защиты при хˉ = 1,5 (остается проход для наружных масс). И только при скорости 5 м/с (εmax = 1,41) ось струи пересекает плоскость проема в координате х̅ = 2,2, что означает близкую реализацию режима полной защиты.
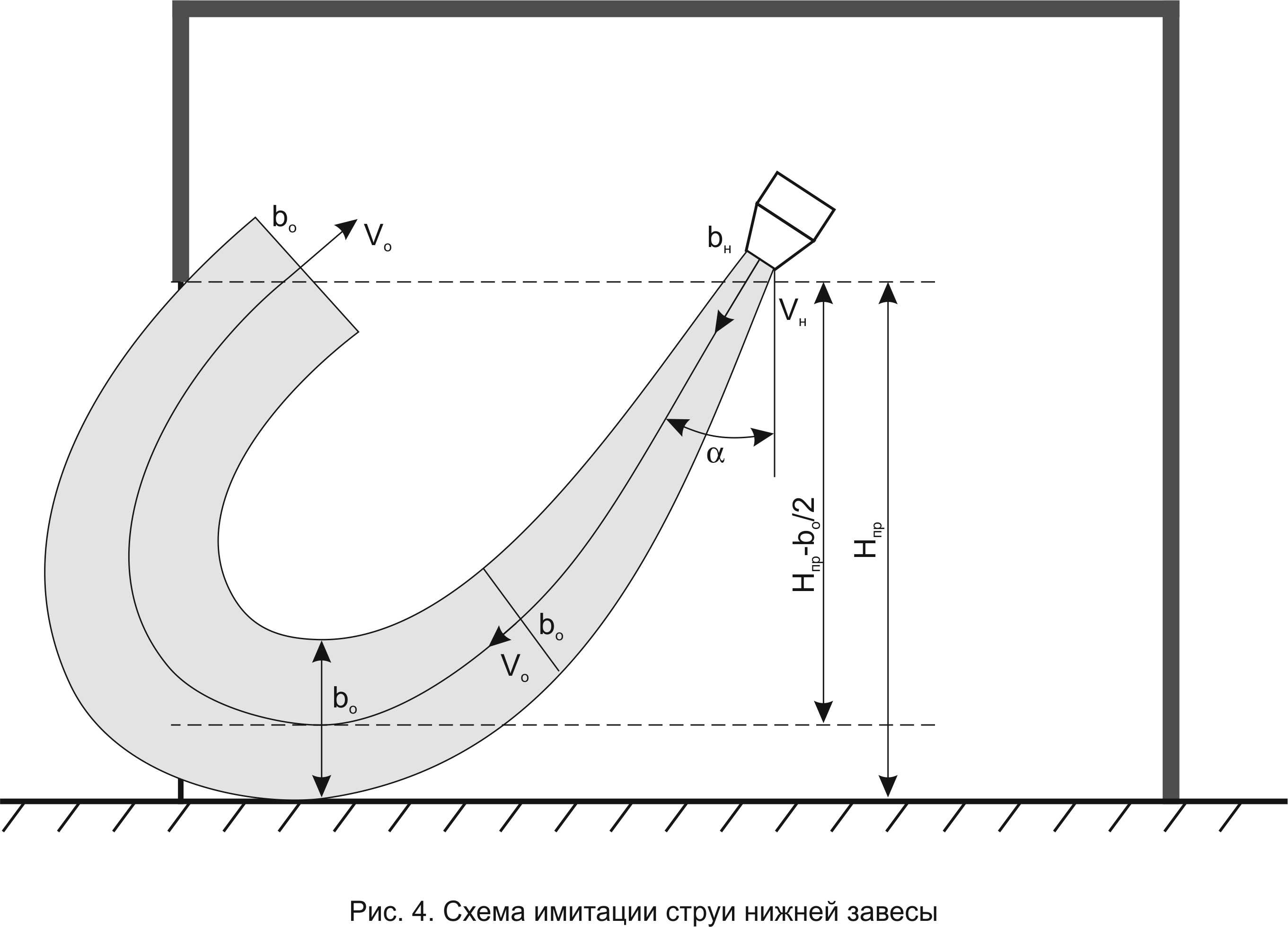
Схема имитации нижней струи завесы представлена на рис. 4. Поток импульса имитированной нижней струи в предыдущем примере для режима полной защиты составляет 192 Н/м. При скорости на выходе из источника 15 м/с это обеспечивается расходом источника 10,7 м3/с/м. Поток импульса противодавления в проеме 338,4 Н/м. Полная защита с таким соотношением потоков импульса возможна, поскольку в рамках данной схемы исходная имитированная нижняя струя направлена под углом 900 к проему и активно отражается от пятна взаимодействия, затекая в проем под углом около 600. Для сравнения, при полной защите верхней завесой с углом струи к плоскости проема 300 потребовался бы двойной ряд аналогичных источников с расходом около 21 м3/с/м и потоком импульса 310 Н/м. Поток импульса предельного режима для верхней защиты 338,4/1,5 = 225,6 Н/м. Превышение потоком импульса верхней завесы потока предельного режима в 310/225,6 = 1,37 раза обеспечивает полную защиту с показателем q = 1. Как видно, имитация нижней завесы с углом струи к плоскости проема 900 позволяет реализовать значительно более экономичную защиту.
Таким образом, удаленные импульсные источники могут быть использованы для организации надежной струйной защиты проемов как прямым лобовым противодействием, так и посредством имитации нижней струи. Реализация такой защиты возможна на основе струйных вентиляторов и мощных промышленных завес типа КЭВ-П8020А, КЭВ-П9010А и КЭВ-П10010А.
Литература
1. Марр Ю. Н. Воздушно-тепловые завесы. Расчет и проектирование завес для защиты проемов промышленных и общественных зданий. СПб.: АО «НПО «Тепломаш». 2017 — 160 с.
2. Гиневский А. С. Теория турбулентных струй и следов. Интегральные метолы расчета. М.: Машиностроение.1969 — 400 с.
3. Теория турбулентных струй. Издание 2-е переработанное и дополненное. Под редакцией Г. Н. Абрамовича. М.: Наука. 1984.
4. Тюменцев В. А. Исследование боковой односторонней воздушной завесы без подогрева воздуха. Автореферат дисс. …к. т. н. Иркутск. 2004.
5. Гиршович Т. А. Турбулентные струи в поперечном потоке. М.: «Машиностроение». 1993.
6. Эльтерман В. М. Воздушные завесы. Изд. 2-е. М.: Машиностроение. 1966.
Скачать статью в pdf-формате: Защита проемов удаленными от створа импульсными струйными источниками