Сайт научно-технического журнала «Инженерные системы. АВОК Северо-Запад»

Еще раз о феномене радиального колеса типа Ц14-46

Ю. Н. Марр, советник генерального директора АО «НПО «Тепломаш»

Радиальные колеса барабанного типа с лопатками, загнутыми вперед, имеют принципиально различающиеся характеристики при их размещении в спиральном корпусе и в свободном состоянии [1]. Обратное влияние спирального корпуса на течение в колесе отмечалось всегда [1, 2]. Однако и в [1, 2], и в более ранних работах его влияние на работу колес ограничено случаем прямого функционального назначения корпуса.

 Анализ экспериментальных работ [3] привел к выводу, что спиральный корпус не только собирает массовый расход и преобразовывает динамическое давление. Он прямо воздействует на формирование потока в колесе с лопатками, загнутыми вперед, упорядочивая аэродинамическую структуру в межлопаточных каналах колеса. Именно этим обеспечивается многократное повышение аэродинамических характеристик вентиляторов с колесами барабанного типа с лопатками, загнутыми вперед.

 Объяснение феномену, данное в [3], показалось нам недостаточным. Поэтому возникла необходимость к нему вернуться.

1.    Факт радикального упорядочения течения в колесе типа Ц14-46 при установке его в спиральный корпус выводит задачу за рамки традиционных представлений о воздействии «здесь и сейчас» и не позволяет называть тривиальным принуждение, которое оказывает спиральный корпус на течение в колесе. Сильное влияние вверх по потоку аэродинамических структур, расположенных за колесом, а также действие положительной обратной связи [3] наводят на мысль о принадлежности феномена к явлениям самоорганизации.

Эта область знаний об эволюции природных объектов и процессов называется синергетикой [4] (см. главу 2, «Синергетика как новая парадигма»). Объектами синергетики являются открытые неравновесные системы. В общем случае такая система представляет собой выделенную область пространства, заполненную некоей средой. Система контактирует с внешним окружением, имеет источники и стоки различных субстанций (массы, вещества, импульса, энергии и т. д.), обменивается субстанциями с внешним окружением. Все процессы в системе можно обозначить одним понятием — перенос субстанций — даже для таких усложненных случаев, как фазовые переходы и химические реакции. Субстанция переносится самопроизвольно от источника к стоку или, предельно упрощая, из области, где ее «много», в область, где ее «мало», из области высокого потенциала в область низкого.

Пока плотности потоков переносимых субстанций малы, сам перенос носит диффузионный характер (теплопроводность, молекулярная вязкость и т. д.). Система считается локально квазиравновесной. Потоковые структуры в таких системах имеют монотонно изменяющиеся параметры. Применительно к ним используют термин «организация», поскольку монотонная структура принудительно и однозначно организована линейными законами переноса субстанций и граничными условиями.

Возрастание интенсивности источников и стоков повышает плотности потоков субстанций — система удаляется от равновесия, однако до поры до времени изменения остаются количественными, новых качеств не возникает. Лишь начиная с некоторого критического момента монотонные потоковые структуры теряют устойчивость и разрушаются. На их месте самопроизвольно возникает новый вид порядка, обеспечивающий перенос субстанций с потоками более высокой плотности. В этой перестройке отсутствуют какие-либо механизмы принуждения и целеполагания, она совершается за счет внутренних стимулов сложной нелинейной системы и обозначается термином «самоорганизация» [4]. Примерами могут служить в теплопереносе ячейки Бенара, в химии — реакции Белоусова — Жаботинского, в гидродинамике — вихри Тейлора, дорожки Кармана и переход от ламинарного течения к турбулентному.

Современные представления о роли самоорганизации в эволюции получили развитие не только в части возможности сверхбыстрого протекания процессов, за которым стоит нелинейная положительная обратная связь. Главное, получил обоснование дуализм эволюции, заключающийся в неразрывной связи энтропийных процессов, направленных к равновесию в соответствии со вторым началом термодинамики (организация), и антиэнтропийных процессов, направленных к неравновесности (самоорганизация) [5]. Завершая короткий экскурс в вопросы синергетики, отметим, что ее возможности сегодня сделали реальностью материалистические объяснения многих парадоксальных явлений, например, даже таких, как будущее организует настоящее [4].

 2. Вентилятор перемещает массу из области пониженного давления в область повышенного. В отличие от описанной системы для организации такого движения требуется затрата механической энергии. Система допускает в своем составе источники любого вида энергии, в том числе кинетической. Передача энергии среде есть процесс, приводящий к появлению макроскопических движений среды, или, попросту, течений. Это переводит рассмотрение в область гидродинамических систем. Простая разность давлений на границах системы приведет к течению жидкости (потоку массы) в направлении уменьшения давления. Направленное введение в систему кинетической энергии может обратить течение жидкости в сторону повышения давления.

Тангенциальные напряжения (на стенках и между спутными течениями) формируют в системе потоковые структуры с диффузионным переносом импульса в пограничных слоях (каналах) или в свободных слоях сдвига. Потеря устойчивости этих структур в соответствующих системах порождает не только упомянутые вихри Тейлора, дорожку Кармана, но и турбулентность, т. е. переход к самопроизвольному хаотическому движению жидкости в макромасштабе с последующей полной диссипацией энергии.

3. В нашем случае передача энергии воздуху осуществляется радиальным колесом барабанного типа с лопатками, загнутыми вперед, с гидравлически короткими межлопаточными каналами. Действие массовых (центробежных) и поверхностных сил формирует протекающий через колесо поток, который в случае свободного колеса почти целиком заворачивает назад в межлопаточные каналы, образуя циркуляционные зоны [3]. Лишь малая часть этого потока выходит из колеса в свободное пространство, формируя расход и избыточное статическое давление. Свободные колеса Ц14-46 можно уподобить перемешивающим устройствам, создающим интенсивное принудительное перемешивание среды. Движение заполняет внутреннее пространство колеса, выходит в его наружную окрестность и поддерживается введением в поток механической энергии с практически полной ее диссипацией (95%). Свободное колесо типа Ц14-46 превращается в гидродинамический нагреватель [1].

Среда, заполняющая свободное колесо и протекающая через него, хаотизирована не только на микроуровне, но и в движениях на макроуровне. Последние поддерживаются непрерывным введением в поток кинетической энергии и приобретают сугубо специфический характер искусственной турбулизации.

 В естественном турбулентном движении структура пульсаций есть результат наложения движений различных масштабов: от самых крупных, порядка размеров системы, до самых мелких, в которых существенной становится вязкость жидкости. Такая структура соответствует представлению о развитой турбулентности [6]. При этом центральным моментом становится переход энергии от турбулентных пульсаций (вихрей) с большими масштабами к пульсациям с меньшими масштабами практически без диссипации. Собственно диссипация, т. е. переход кинетической энергии в тепло, происходит в самых мелкомасштабных (вязкостных) пульсациях.

Модель развитой естественной турбулентности [6] была успешно использована в перемешивающих устройствах для обоснования зависимостей тепло- и массопереноса [7]. Это означает, что в пространстве масштабов искусственно турбулизированной жидкости также возникает непрерывный поток энергии от крупно- к мелкомасштабным пульсациям. В физическом пространстве между каналами лопаточной решетки и внутри них на фоне всеобщего хаотического пульсационного движения будут просматриваться рециркуляции массы с незначительными отслоениями и протоками за пределы колеса. Гипотетически эти протоки можно рассматривать как результат случайных возмущений потока энергии в пространстве масштабов. Из них складывается расход свободного колеса. Чем сильнее возмущения в пространстве масштабов, тем выше уровень порядка в физическом пространстве и больше расход через колесо. В пределе полное подавление макроскопического хаоса восстанавливает структуру течения в колесе в спиральном корпусе.

 Таким образом, гипотетически полная потоковая структура свободного колеса представляет собой сопряженные потоки двух субстанций: кинетической энергии в пространстве масштабов и массы в физическом пространстве через межлопаточные каналы колеса.

 4. Обычно рассматривают раздельно два крайних случая: свободное колесо и вентилятор. Вместо этого зададим открытую неравновесную систему в виде радиального колеса, вращающегося в пространстве с варьируемым ограждением, в котором имеется регулируемый выход воздуха наружу. Выбрасываемый колесом поток воздуха создает в пространстве за колесом вращающееся кольцевое течение (крутку). Ограждение может быть удаленным от колеса настолько, что колесо остается свободным. В этом случае кольцевое течение принимает форму относительно вялой раскручивающейся веерной струи. Приближение ограждения к колесу с постепенным приданием ограждению спиралевидной формы переформировывает свободный поток из колеса, усиливая крутку.

По мере приближения ограждения к колесу скорость и масштаб крутки нарастают. Предельная конфигурация ограждения — спиральный корпус — завершает перестройку кольцевого течения в потенциальный вихреисточник. Это течение подтверждено измерениями на выходе из колеса в спиральном корпусе [1]. Его ядро занимает около 70% ширины колеса вблизи заднего диска. Величина тангенциальной составляющей скорости c̄_2u лежит в диапазоне от 1,6 до 2,1 при коэффициентах расхода φ = 0,35 – 0,7. В области оставшихся 30% ширины колеса (у переднего диска) возникают возвратные течения, особенно при малых расходах. По измерениям [8] тангенциальная скорость ядра потока в спиральном корпусе составляет c̄_3u = 1,2 – 1,5.

По отношению к течению внутри колеса вращающийся поток за колесом можно рассматривать как внешний независимый фактор системы, оказывающий кольцевое тангенциальное воздействие на структуру течения в колесе. Внешний организующий фактор определяет положение системы на термодинамической ветви, т. е. степень удаления системы от термодинамического равновесия и приближения ее к режиму с критической плотностью потока переносимой субстанции. В нашей системе, как было сказано, одной из сопряженных переносимых субстанций является проток массы через колесо, из которого формируется охватывающая колесо крутка. Малейшая активизация крутки, обусловленная приближением ограждения и связанная, в первую очередь, с увеличением угла выхода потока из колеса в относительном движении, посылает вверх по потоку (в межлопаточные каналы) информацию о возникшем несоответствии имеющего место в колесе течения требованиям локализованной ниже по потоку крутки. В связи с этим можно говорить о приходе системообразующей информации из «будущего» в структуру, «живущую сейчас» внутри колеса.

Применительно к явлениям гидродинамики в этом утверждении нет ничего из ряда вон выходящего. Когда масштабы наблюдаемого позволяют одномоментно охватить все, что происходит ниже по течению и выше по течению, возникает очевидная аналогия с ходом времени. Появляется «настоящее» — структура, расположенная в данном месте, «прошлое» — структура выше по течению и «будущее» — то, что ниже, дальше, потом. Моделирование взаимодействия «будущего» с «настоящим» — отдельная задача синергетики, имеющая материалистическое толкование [4]. Здесь речь будет идти только о гидродинамической интерпретации такого взаимодействия.

5. На основе организующего фактора определяют так называемый управляющий параметр. В гидродинамике это, большей частью, число Рейнольдса, в свободной конвекции — число Релея. По достижении критического значения параметра потоковая структура теряет устойчивость, флуктуации разрастаются, и система переходит на другую ветвь развития. Управляющий параметр нашей неравновесной системы связан с кольцевым тангенциальным воздействием, в частности, со степенью опережения кольцевой круткой вращения колеса. Можно принять в качестве управляющего параметра коэффициент тангенциальной скорости на выходе из колеса c̄_2u и рассматривать тангенциальное воздействие в режимах превышения тангенциальной проекцией линейной скорости вращения колеса c̄_2u ≥ 1. Существует некоторое критическое значение (c̄_2u)_кр, при котором потоковая структура свободного колеса станет неустойчивой и начнется выстраивание порядка.

Флуктуации потоковой структуры на основе молярного переноса, по всей видимости,

представляют собой локальные случайно возникающие нарушения в пространстве масштабов, оборачивающиеся в физическом пространстве очагами регулярных движений. В свободном колесе таковыми можно считать беспорядочные выбросы воздуха, образующие в среднем расход колеса. Устойчивость потоковой структуры к флуктуациям обеспечивается у свободного колеса стабилизирующим воздействием относительно вялой быстро раскручивающейся веерной струи с управляющим параметром не более единицы. Даже небольшая активизация крутки на выходе из колеса (увеличение управляющего параметра c̄_2u) усилит флуктуации, т. е. увеличит их частоту, продолжительность и объем областей регулярного движения в колесе. Внутри них начнут развиваться элементы структурированного течения в межлопаточных каналах, которые приведут к росту расхода и дополнительному увеличению управляющего параметра c̄_2u.

6. Наиболее частый случай взаимодействия «будущего» и «настоящего» — это распространение вверх по потоку информации-импульсов давления, которые переформировывают набегающий поток, готовя его к контакту, например, с расположенным впереди обтекаемым телом или перетеканием в канал другой формы и направления. Такого рода влияние будущего на течение в колесе вентилятора наглядно демонстрируется системой «колесо — ограждение» на основе одномерной симметричной модели течения в колесе и в корпусе без потерь [1, 2].

Обычно по заданному углу выхода потока из колеса (абсолютной скорости) α₂₀ определяют требуемые размеры спирального корпуса: раскрытие обечайки А̄ = А/D₂, ширину корпуса В̄ = В/D₂. Обратим логику задачи. При заданных размерах корпуса и реализации в нем течения типа вихреисточника будем искать требуемый угол выхода потока из колеса. Расчетная зависимость имеет тот же вид, что и для прямой задачи [1, 2]:

tg α₂₀ = (1/2π) (В̄ / b̄₂) ln (1 + 2А̄). (1)

При выводе выражения (1) геометрия колеса не оговаривалась. Было лишь обозначено, что на выходе из колеса имеют место составляющие скорости с_2r и c_2u, связанные с углом выхода потока равенством

c_2u = с_2r сtg α₂₀, (2)

которое с учетом (1) становится характеристикой спирального корпуса. Поэтому (1) справедливо для любого колеса. Смысл его состоит в том, что в колесе (т. е. в «настоящем») должна установиться такая структура, которая независимо от угла выхода лопатки β₂ обеспечит угол выхода потока, требуемый сложившимся в заданном корпусе течением (т. е. «будущим», поскольку корпус расположен по потоку ниже колеса). Режим с этим углом выхода называют режимом согласованной работы колеса и корпуса (можно перефразировать в «режим согласованного c будущим настоящего»). Показано [1, 2], что при идеальной характеристике свободного колеса, имеющей вид

c̄_2u = 1 – c̄_2r ctg β₂, (3)

коэффициент радиальной скорости для реализации режима согласованной работы должен равняться

c̄^c_2r = (ctg β₂ + ctg α₂₀) ^-1. (4)

Выражение (4) получается как пересечение характеристики корпуса (2) с характеристикой колеса (3) в координатах c̄_2u, c̄_2r. Таким образом, для режима согласованного взаимодействия «настоящего» с «будущим» необходима «самоподгонка настоящего», которая протекает в рамках предсказуемости в соответствии с (3), является очевидным результатом принуждения по (1) и поэтому не имеет отношения к самоорганизации.

Подобных примеров в технике много. У тех же вентиляторов рабочая точка определяется пересечением характеристики вентилятора и характеристики сети. Применительно к нашей гидродинамической аналогии хода времени вентилятор — объект «настоящего». Сеть, независимо от расположения ее относительно вентилятора, есть объект «будущего», поскольку требования сети первичны по отношению к возможностям вентилятора и его реакции. Здесь «будущее» (сеть) точно так же принуждает «настоящее» (вентилятор) занять детерминированную рабочую точку.

7. Характеристики свободных колес барабанного типа не описываются выражением (3), и поэтому рассмотренное выше согласование не имеет места. Для описания взаимодействия колеса со спиральным корпусом требуется моделирование перестройки течения в колесе. Покажем, как можно моделировать данную ситуацию на основе тех же выражений (1) — (4) с идеализированным одномерным течением. Для этого расширим систему «колесо — ограждение» возможностью варьировать геометрию колеса, в частности, изменять угол выхода лопаток β₂* (звездочкой отмечена варьируемость угла). Этим достигается возможность приближенно моделировать происходящее в реальном колесе отклонение угла выхода потока в относительном движении от угла выхода лопатки β₂ через угол β₂*. В целом можно наблюдать самоперестройку всей структуры от свободного колеса до колеса внутри спирального корпуса. При этом ограждение всегда остается в форме спирального корпуса, и при любых размерах в нем развивается течение типа вихреисточника. Ситуация свободного колеса приближенно моделируется ограждением с большой величиной раскрытия, например, А̄ >10.

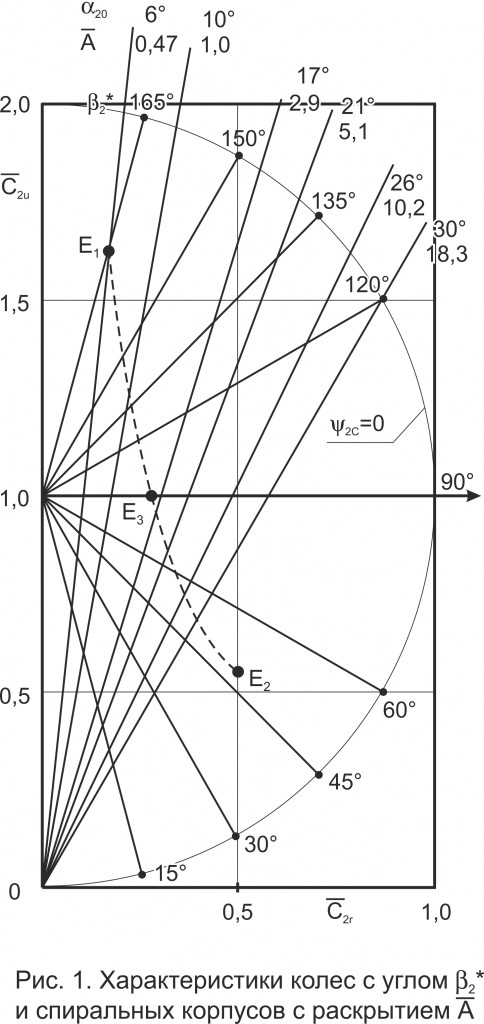
Перенесем рассмотрение в поле характеристик в координатах c̄_2u, c̄_2r на рис. 1. Прямые, исходящие из точки (1,0), — характеристики радиальных колес, имеющих углы выхода β₂* в диапазоне от 15⁰ до 165⁰. Лучи, проведенные из начала координат, — характеристики спиральных корпусов с углами входа α₂₀ от 6⁰ до 30⁰ и соответствующими им раскрытиями А̄ от 0,47 до 18,3 (далее всюду принято В̄ / b̄₂ = 1).

 Относительно характеристик колес следует оговориться. В [1, 2] под выражением вида (3) подразумевается характеристика свободного колеса. Для колес с лопатками, загнутыми назад (β₂* < 90⁰), это справедливо, поскольку их реальные характеристики мало отличаются от ситуации расположения в спиральном корпусе. Для колес с лопатками, загнутыми вперед (β₂* > 90⁰), характеристики свободных колес не имеют ничего общего с видом (3). Поэтому их условные изображения на рис. 1 следует понимать для ситуации расположения колес внутри спирального корпуса. Поле возможных режимов с положительным статическим давлением на рис. 1 ограничено линией полуокружности с радиусом c̄_2r = 1, на которой коэффициент статического давления равен нулю, что соответствует условию

(c̄_2r)_max ≤ sin β*₂. (5)

Все точки пересечения характеристик одного семейства с другим внутри границы (5) есть режимы согласованной работы колеса с корпусом (4).

Рассмотрим вначале процесс удаления ограждения от колеса. Выберем в качестве исходного варианта точку Е₁ для колеса с β₂ = 165⁰ в спиральном корпусе с раскрытием А̄ = 0,47 (α₂₀ = 6⁰). Для моделирования перевода колеса в свободное состояние начнем увеличивать раскрытие корпуса, принимая во внимание требование варьируемого вихреисточника к изменению положения согласованного режима внутри области (5). Понятно, что с ростом А̄ точка Е начнет перемещаться вниз по некоторой траектории, уменьшая угол β*₂. Зададим условие вариации, например, в виде постоянной относительной аэродинамической мощности системы

N̄_a = (c̄_2u) (c̄_2r) = const. (6)

В исходной точке N̄_a (Е₁)= 0,277. Траектория постоянной мощности с этим значением изображена на рис. 1 пунктирной линией. Она достигает минимального угла в области колес с лопатками, загнутыми назад (ориентировочно при β*₂ = 50⁰ , А̄ ≈ 267 и α₂₀ ≈ 45⁰), — точка Е₂, что соответствует очень сильному отклонению потока от β₂ = 165⁰ в относительном движении. Поскольку в реальном свободном колесе Ц14-46 такое отклонение достигает угла 90⁰ [3], логично прервать траекторию в точке Е₃ ее пересечения с характеристикой колеса при β*₂ = 90⁰.

Можно интерпретировать этот результат следующим образом. Перенос колеса с углом β₂ =165⁰ из согласованного спирального корпуса (точка Е₁) в практически свободное пространство, в котором влияние вихреисточника исчезающе мало (точка Е₃, величина раскрытия около 2,8), резко уменьшает управляющий параметр c̄_2u от 1,65 до 1. А это изменяет требования к формированию выходящего из колеса потока в сторону упрощения структуры путем увеличения угла выхода абсолютной скорости α₂₀ до 16,5⁰ в точке Е₃. В рамках разрешенной нашей системой трансформации такое увеличения угла α₂₀ становится возможным только при значительном уменьшении угла выхода лопатки β*₂ (или угла относительной скорости).

Полученный результат демонстрирует хорошее качественное совпадение с реальной ситуацией в части угловых параметров. Однако идеальная модель одномерного движения без потерь, да еще при условии неизменной аэродинамической мощности, не допускает полного качественного совпадения с реальностью. Так, угол 90⁰ в реальном свободном колесе сформирован не трансформированными лопатками колеса, а отрывными циркуляционными зонами, угнездившимися в каналах круговой решетки. Расход (c̄_2r) в идеальной модели при перемещении к точке Е₃ не уменьшается, а увеличивается. И хотя последнее обстоятельство не так далеко от истины, в рамках данной модели невозможно отразить возникающую в свободном колесе мощную рециркуляцию масс и затрачиваемую на это энергию (потери) с многократным уменьшением полезной аэродинамической мощности. Поэтому главный результат моделирования — это перестройка течения в колесе с изменением угла выхода потока.

В конечном счете нас интересует траектория обращенного движения точки Е от почти свободного колеса до его нормального размещения в спиральном корпусе. Соблюдение условия (6) гарантирует идентичность траектории Е₃ – Е₁ с увеличением управляющего параметра c̄_2u и угла выхода β*₂. Обращенная трансформация структуры потока в колесе, названная выше «самоперестройкой» и опирающаяся на трансформацию круговой решетки, может рассматриваться как упрощенный аналог самоорганизации под действием внешнего фактора — интенсивности крутки охватывающего колесо потока. Термин «самоорганизация» используется здесь с оговоркой, поскольку описанная самоперестройка — результат жесткого модельного детерминизма. При этом рост формального в данном случае управляющего параметра c̄_2u напрямую связан с уменьшением величины раскрытия корпуса А̄.

8. Информация из «будущего» диссипативной системы — это, в конечном счете, отрицание возможности существования в «настоящем» монотонных потоковых структур. Как это происходит?

 Под действием внешнего организующего фактора возрастающая плотность потоков субстанций в существующих структурах достигает критического значения. С дальнейшим усилением воздействия возникает рассогласование между требуемым результатом переноса субстанций и реально проходящим на пределе возможного потоком. Допуская некоторую образность выражений, можно уподобить диссипативную систему конструкции «сеть — насос» и говорить о «вакууме будущего» из-за доведенной до предела «сети настоящего». Рассогласование между требуемым и предельно возможным есть один из тех внутренних стимулов сложной нелинейной системы, который ставит вопрос о радикальном изменении характеристики «сети настоящего», т. е. видоизменении самой сети. Он и включает механизм случайных возмущений. Малые возмущения перестают рассасываться, нарастают и переходят в нелинейную стадию развития, полностью деформируя потоковую структуру. На ее месте без какого-либо принуждения самопроизвольно формируется новая «сеть», соответствующая «вакууму будущего» и позволяющая реализовать перенос с бóльшими плотностями.

 Факт радикального влияния «будущего» на «настоящее» не является чем-то уникальным. В синергетике формирование ячеек Бенара есть не что иное, как реагирование жидкой среды на «требование» пропускать поток тепла более высокой плотности от горячего источника к холодному. Здесь и свершается «будущее» в рамках заданной системы — диссипация тепловой энергии в холодном источнике.

 Движение тела в жидкой среде — один из наиболее ярких примеров гидродинамики. В масштабах движущегося тела жидкость считается сплошной средой (реальная дискретность на микроуровне). Однако в передней критической точке тела сплошность среды нарушается. Завихренные телом слои жидкости разъединяются и растекаются. После отрыва слоев от тела и перехода в свободное состояние из них формируются макроскопические жидкие структуры (вихревые зоны), в которых происходит перенос массы, импульса и энергии, направленный на придание вихревым движениям такого вида, при котором, по возможности, быстрее рассеивались бы квазинарушения сплошности. С возрастанием интенсивности таких нарушений (при больших числах Рейнольдса) движение жидкости за телом принимает автоколебательный характер: образуется шахматная вихревая дорожка Кармана. «Настоящее» частиц жидкости с той или с другой стороны движущегося тела определяется «будущим» в виде периодического воздействия образующихся и отрывающихся вихрей за телом и изменения циркуляции на нем.

 Важнейшим аспектом практически всех случаев самоорганизации систем является повышение масштаба кажущейся дискретности среды. Сплошная среда заполняется немонотонными макроструктурами: вихрями Кармана, ячейками Бенара, в турбулентности — каскадом вихрей с убывающим масштабом.

Упорядочение течения в межлопаточных каналах колес барабанного типа демонстрирует такой же эффект повышения уровня дискретности среды. Масштабы геометрические, временные, импульса и кинетической энергии струй, истекающих из межлопаточного пространства, значительно превышают соответствующие аналоги вихревых образований свободного колеса.

9. Поступление информации из будущего включает, в нашем случае, положительную обратную связь между структурами в межлопаточных каналах и наружным вихреисточником. Посыл в колесо структурирующей информации приводит к росту порядка (увеличению расхода, уменьшению угла выхода потока в относительном движении), а это, в свою очередь, способствует дальнейшему формированию вихреисточника и усилению его тангенциального воздействия. Возвращаясь к образным толкованиям, вихреисточник, как инициатор «вакуума будущего», изменяет характеристику «сети настоящего», увеличивая ее пропускную способность. Этим подпитывается интенсивность вихреисточника и неослабевающий «вакуум будущего». Положительная обратная связь помогает совершить эту метаморфозу в ускоренном режиме. Поэтому переход к ограждению типа спирального корпуса практически скачком преобразовывает течение в колесе к виду, обеспечивающему характеристику типа (2) и режим согласованной работы колеса и корпуса в смысле выполнения условий (1) и (4).

10. Рассмотренные здесь аспекты феномена колес барабанного типа дают ясное понимание невозможности воспроизвести феномен без течения типа вихреисточника, охватывающего снаружи колесо и имеющего тангенциальную скорость, превышающую скорость вращения колеса. Оказалось, что в отсутствие спирального корпуса никакие конструктивные ухищрения не способствуют сколько-нибудь заметному приближению к характеристикам стандартного вентилятора. Размещение колеса с лопатками, загнутыми вперед, в прямоугольном или круглом корпусе (опыты автора) по аналогии с прямоточными радиальными вентиляторами [9] имеет нулевой эффект. Установка в той же конструкции вокруг колеса четырех спиральных лопастей (опыты автора) ничего не добавляет к предыдущему результату. В варианте с вращающимся вместе с колесом радиальным безлопаточным диффузором — продолжением колеса [1] намечается небольшое улучшение характеристики. Однако и этот результат далек от колеса в спиральном корпусе. Возможно, вращение отделенного от колеса диффузора с частотой, большей частоты вращения колеса, могло бы добавить упорядочение течения в колесе и повысить характеристику. Однако конструктивное усложнение варианта не сможет оправдать предполагаемый результат.

ВЫВОДЫ

Феномен радиальных колес барабанного типа, состоящий в разительном отличии характеристик свободного колеса и колеса в спиральном корпусе, имеет прямое отношение к явлениям самоорганизации. Скачкообразная трансформация структуры потока в колесе с таким же скачкообразным ростом характеристик при переносе колеса в спиральный корпус есть результат упорядочения, лишенный прямого принуждения заданной геометрией колеса и действующими силами. Один из главных стимулов — это информация, распространяющаяся вверх по потоку из внешнего к колесу пространства и способствующая поддержанию упорядоченного течения в межлопаточных каналах. Генератором стимулирующей информации является развитое течение типа вихреисточника, охватывающее снаружи колесо и имеющее тангенциальную скорость, превышающую скорость вращения колеса. Именно по этой причине никакие

конфигурации окружающего колесо пространства, не создающие потока, вращающегося быстрее колеса, не могут воспроизвести феномен. В отсутствие спирального корпуса этому могут лишь частично способствовать конструкции типа вращающегося диффузора.

Литература

1. Соломахова Т. С. Радиальные вентиляторы: Аэродинамика и акустика/Т. С. Соломахова; Центральный аэрогидродинамический институт имени профессора Н. Е. Жуковского. — М.: Наука, 2015. — 460 с.

2. Соломахова Т. С. К расчету спирального корпуса центробежного вентилятора // Промышленная аэродинамика. Выпуск 2 (34). 1987. — М.: Оборонгиз, с. 77–85.

3. Марр Ю. Н. О взаимодействии радиального колеса с лопатками, загнутыми вперед, со спиральным корпусом. Инженерные системы — АВОК — Северо-Запад. № 3. 2019. С. 10–14.

4. Князева Е. Н., Курдюмов С. П. Законы эволюции и самоорганизации сложных систем. — М.: Наука, 1994. — 236 с.

5. Руденко А. П. Самоорганизация и синергетика. АНО «Центр междисциплинарных исследований» (ЦМИ) [Электронный ресурс]. Режим доступа: Сайт С. П. Курдюмова. (дата обращения 15.01.2020).

6. Ландау Л. Д., Лифшиц В. М. Гидродинамика. Теоретическая физика. Т.VI. — М.: Наука. 1988. — 736 с.

7. Барабаш В. М., Брагинский Л. Н. Об оценке интенсивности тепло- и массообмена в потоках с искусственной турбулизацией. — ИФЖ, 1981, т. ХL, № 1, с. 16–18.

8. Коваленко В. М. О работе спиральных кожухов центробежных вентиляторов // Промышленная аэродинамика. Выпуск № 17. Вентиляторы. — М.: Оборонгиз. 1960.

9. Караджи В. Г., Московко Ю. Г. Вентиляционное оборудование. Технические рекомендации для проектировщиков и монтажников. — М.: АВОК-ПРЕСС, 2010. — 432 с.

Скачать PDF версию статьи «Еще раз о феномене радиального колеса типа Ц14-46»